A pendulum simulator

download pendulum simulator program

This pendulum exerciser is a small Delphi project.

Below is a reduced picture:



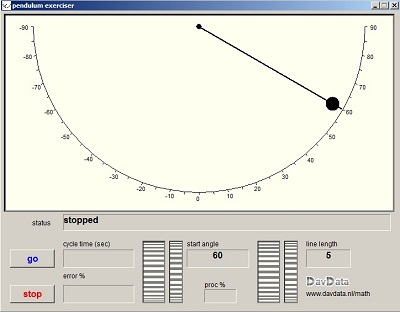
The vertical rotation buttons allow for the selection of the angle at with the mass is released initially
and the length of the cable.

Operation

    - select angle (move mouse over rotation buttons)
    - select line length (..)
    - press go button to release mass

Press stop to end the simulation process.

Displays show:
    - cycle time
    - accuracy of the simulated movement
    - percentage of time the processor needs for the simulation and display
Download this (Windows) program by a click on the lightning icon above.

Note: This simulation does not take air friction into account.

Basic kinematics

The unity of length is the meter (m).
The unity of time is the second (sec).

For constant motion:
distance = speed * time.
s = vt {s : distance (m), v : velocty (m/sec), t : time (sec)}

Acceleration is velocity change per second.
In case of constant acceleration:
v = at {v: velocity (m/sec), a: acceleration (m/sec^2), t: time (sec)}



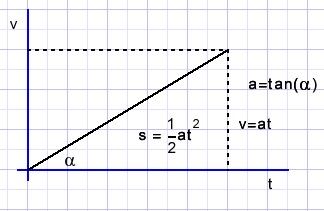
Distance s is the area of the triangle:
    s = 0.5at2
For constant acceleration:
If vt is the velocity of an object at time t:
    vt = v0 + at
If st is the distance in time t
    st = v0t + 0.5at2
The unity of mass is the kilogram, which is independent of gravity.
The unity of force is the Newton
One Newton (N) is the force that accelerates a mass of 1 (kg) by 1m/sec for each second.

F = ma {F: force (N), m: mass (kg), a: acceleration (m/sec2)}
On earth, a = 9.8 and is called g.

Mechanical energy is the product of force and distance:
The unity of energy is the Joule (J).
E = Fs {E: energy (J), F force (N) s: distance (m).

To lift a mass m over h meters upward against gravity takes energy
    Ep = mgh {Ep: potential energy (J)}
Energy is never lost but may be converted to another form such as chemical energy in batteries or heat.
A mass m is accelerated a (m/sec2) during t seconds.
The distance s = 0.5at2.
Energy E = Fs = F*0.5*at2
Since F=ma:
E = 0.5ma2t2
since v=at:
Ek = 0.5mv2 (Ek : kinetic energy (J)}

The simulation process

In the pendulum no energy is lost (theoretically) but potential and kinetic energy alternate.
In the bottom position all energy is kinetic, at the most upward position all energy is potential.
In between these positions there is a mix.
Since the total energy is constant we are able to calculate the exact speed at all heights of the mass.

Speed direction is perpendicular to the radius.
The mass is accelerated by the force perpendicular to the radius.
Forces in the rope take no energy as long as the rope is rigid.



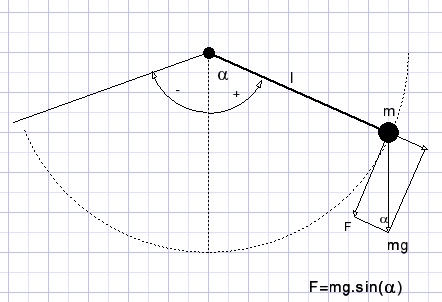
We notice that force F depends on angle α
When measuring α in radians:
    s := αl {s: distance on circle perimeter, l: length of line}
The simulation process is amazingly simple.
Time is subdivided in microseconds.
During this small interval, force F and velocity v are supposed constant.
F is known from angle α and causes acceleration a = F/m = g.sin(α);
So the new velocity v becomes v + a*10-6.
Distance s in this period is v.10-6
and since s = αl
the new angle α becomes α + vt/l.

After 10000 steps, a new picture is presented showing the position of the pendulum.
So, 100 pictures per second are displayed.

Speed and height relation




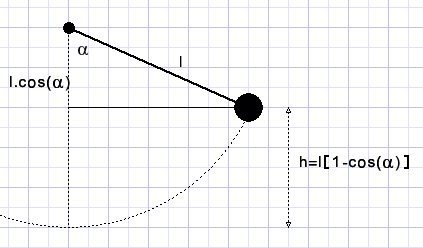
Released at an angle of α at h meter above the lowest point the potential energy is mgh = mgl[1-cos(α)].
At an angle of φ the potential energy is (reduced to) mgl[1-cos(φ)].
This energy loss is now kinetic energy so:



The simulator program uses this formula to check the accuracy:
At maximum speed the kinetic energy should be equal to the potential energy at the start.

An integral for the cycle time

Traveling distance Δs at speed v during a very small time Δt over the circle perimeter: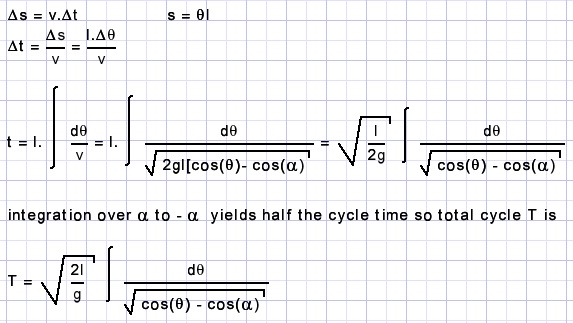



This integral is difficult to solve.

Special case: very small α

Writing cos(x) = 1 - 2sin2(x/2) :
    cos(φ) - cos(α) = 2[sin2(α/2) - sin2(φ/2)]
changes the cycle time integral to



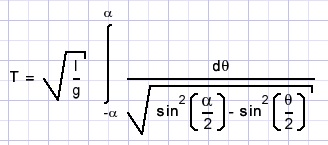
Now substituting



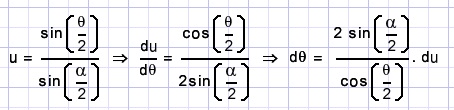
we get:



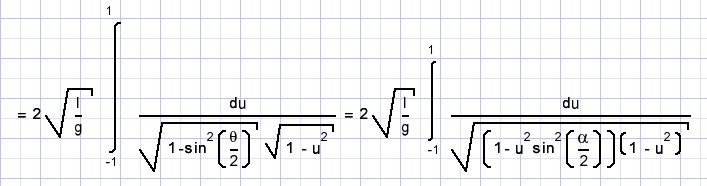
When α is small this integral may be reduced to



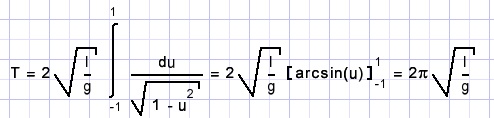
Interested in the Delphi (7) project?

load project code

This project use two of my own components:

1. a microsecond timer



2. a rotation button: