

| A paths problem |
On Facebook group “Classical Mathematics” I found the following problem:
Find the number of paths from A to B in the next image.
Paths may not cross and must pass every square.
One possible path is shown below:
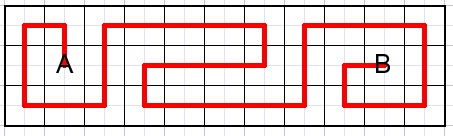
Above picture counts 11 columns and three rows.
To analyze this problem it is helpfull to reduce the problem to less columns.
So I wrote a program that counts the paths for 4 to 15 columns.
This is what the program looks:

The computer shows the first path in a figure with 8 columns.
Pressing the GO button starts the search.
To find more paths, press the SPACE button.
In STEP mode, every new path is showed.
When stepmode is not checked, the program just counts the paths, but does not display.
Program description
The program is written in Delphi-7.Squares are numbered as shown below for an 11 column puzzle:
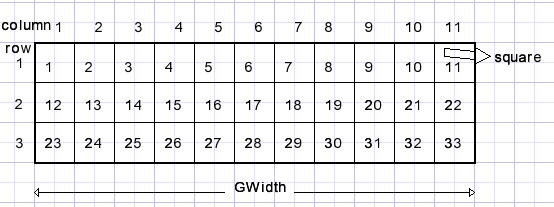
A path is recorded in array paths[ ] as square number-direction, square number-direction.
SquareA is the first square of the path (13), squareB is the last square (21).
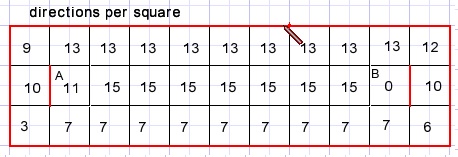
For every square there is a number dirs which has a bit (0,1,2,3) set per allowed direction:
(red lines may not be crossed)
Dataformats
type Tsquare = record
col : byte; //column of square
row : byte; //row ..
dirs : byte; //allowed entry/exit directions
//1:right; 2:up; 4:left; 8:down
full : boolean; //path present
end;
TsearchResult = (srStart,srCnt,srOK,srEnd);
Tstep = record
pos : byte; //place of square
dir : byte; //direction 1,2,4,8
end;
var bm : Tbitmap;
square : array[1..45] of Tsquare; //directions, col, row,
// pah preset
Gwidth : byte = 4; //number of columns
//-- path finding --
path : array[1..45] of Tstep; //square and direction per
//step
pathlength : byte;
pathcount : longword;
search : TsearchResult;
squareA : byte;
squareB : byte;
searchBusy : boolean;
Functions and procedures
procedure setDimension;Erases part of form1.canvas.
Sets Gwidth, bitmap.width, sets column and row fields in array square[ ]
Sets dirs fields of squares. Sets pathlength = 3*Gwidth.
procedure clearPath;Erases the Path[ ] array. Sets full flag to false in square[ ]
procedure procSearch;Controls the search for paths.
Calls function findPath(sr) : Tsearchresult;
Tsearchresult : srStart : search for 1st path (parameter)
srOK : path found (result)
srCnt : search next path (paramameter)
srEnd : no path found (result)
function findpath(sr : TsearchResult) : Tsearchresult;
label nextstep,teststep,nextdirection,stepBack;
var xdir,nextpos,xpos,step : byte;
This function does the search.Xdir : current direction
Xpos : current square
nextpos : next square in path
step : increment for each new square in path, index into path[ ]
To know if a direction out of a square is not allowed this check is made:
if (square[xpos].dirs and xdir) = 0 then goto nextdirection;To see if a square already holds a path:
if square[nextpos].full then goto nextdirection;A path is recorded in array path[1..pathlength].
The dir fields of path[ ] make a counter which counts systematically, no path is missed.
Counting per Xpos is 1..2..4..8
If direction Xdir is allowed and the next square holds no path then the step is recorded:
path[step].dir := xdir; inc(step); path[step].pos := nextpos; xpos := nextpos; square[xpos].full := true;If no step is possible then we go back one step to try a next direction:
if step = 1 then begin result := srEnd; //no path found exit; end; square[xpos].full := false; dec(step); xpos := path[step].pos; xdir := path[step].dir; goto nextdirection; end;next direction code is:
xdir := xdir shl 1; if xdir > 8 then goto stepback; goto teststep;
Search flowchart
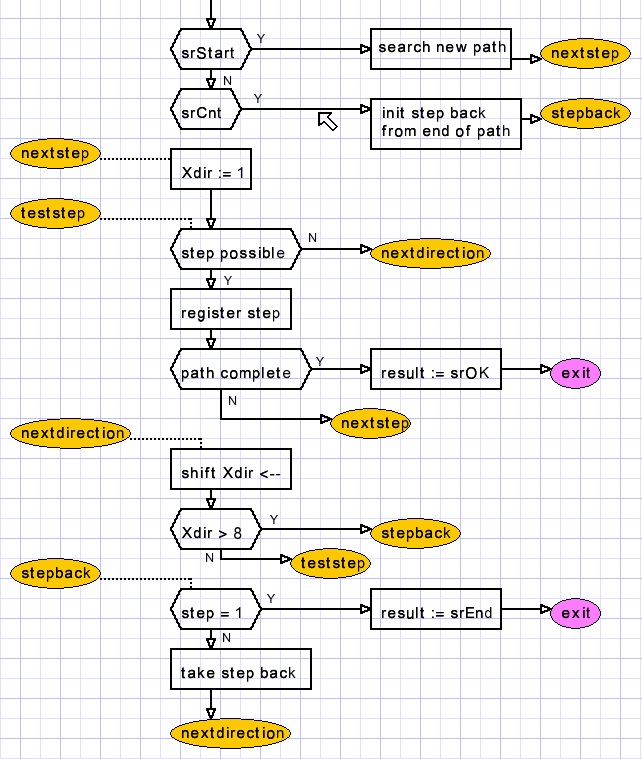
For details please refer to the source code.
Results
| columns | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| paths | 2 | 6 | 14 | 30 | 62 | 126 | 254 | 510 | 1022 |
| path+2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
| (path+2)/2^(n-2) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
So:

This formula P(n) for the number of paths per n columns is valid for
columns 4 .. 12 as calculated and likely also for any higher more column counts.
But for n > 12 there is yet no full proof.
Analyses
For reasons of simplicity we cut the number of path in half by allowing onlyright directions in square 2.
Pink lines are drawn to divide the puzzle in sections.
The path always tries to expand in the right direction.
4 columns
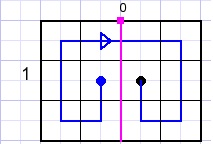
We find 1 path.
The pink line separates the puzzle in two sections but has no effect on the path.
5 columns
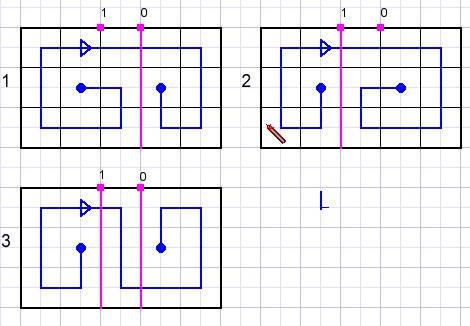
3 paths.
Two pink lines are possible. Zero pink lines results in the same path as line 1( bit 0 set).
6 columns
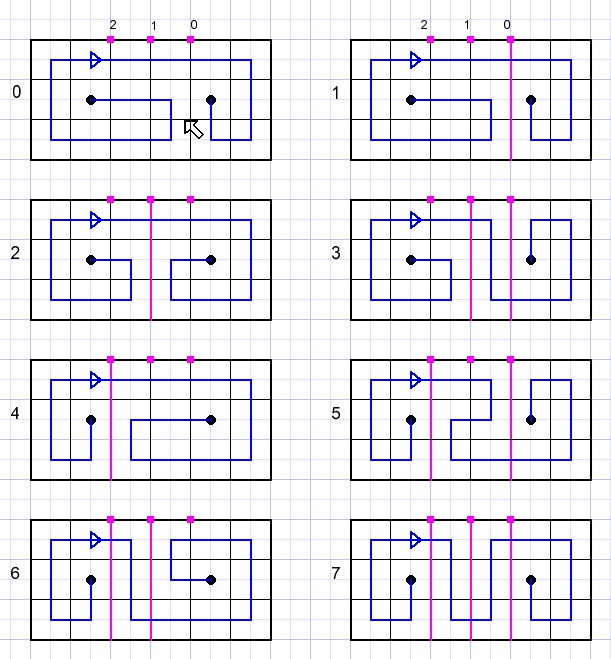
Seven paths.
Note: path 0 and 1 are identical.
Conclusion
In a n column puzzle up to n-3 pink lines may be drawn which can be done in 2^(n-3) ways.The pink lines separate the puzzle in sections.
Rule: do not leave a section until the road crosses all squares of the section.
If P(n) is the number of paths for a n columns puzzle then
(allowing left direction in square[2] which doubles the paths)

