Equations of circles and ellipses

This article describes translation, scaling and rotation of circles and ellipses.
First some definitions:

variablea character such as x or y, a number that may change
constanta fixed value such as 3, -5 but also a, b or x1, y1
formulaa arithmetic expression with variables
equation a construct with format formula = formula

A function is a special case of an equation.
    y = ...x.....
Left of the "=" character is one variable only, the result of the formula right of the "=".
The "..." stand for operations and constants.
x is called the independent and y the dependent variable.
x is assigned a value and for each value of x y may be calculated.
A function has exactly one number as result so functions may be part of a formula.

Examples of formulas are:
3x2 + 5y2
7x - 8y - 10.

An example of an equation is:
3x2 + 5y2 = 2x - y + 25

Some examples of functions are:
y = 3sin(x)
y = 3x3 - 2x2 + x - 7

Graphics

Graphics are pictures of equations and functions.
Take equation x2 + y2 = 1

For a value of x the value of y may be calculated.
Writing these number pairs as (x,y) they become coordinates in a plane.
For each (x,y) pair we may paint a dot.
For the case above this results in:



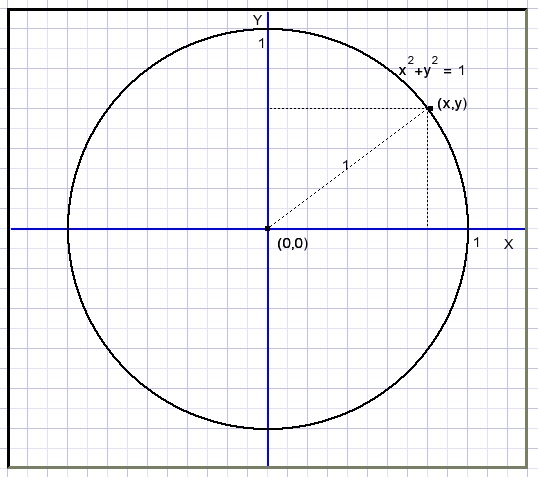
A circle with center (0,0) and radius 1.
The Pythagoras theorem shows why.

Translation

The center of the circle may be at another place than (0,0).
What would happen to the equation in this case?
We apprpoach the translation (shifting) ploblem in a general way.

Say we have an undefined equation ..x..y.. = ..x..y.. and point (x1,y1) is a point on the graph.
Next we replace (x) by (x+1) and (y) by (y+2).
The result is ..(x+1)..(y+2) = ..(x+1)..(y+2)
Say point (x2,y2) is on the new graph.
This will be the case if :
    (x2 + 1) = x1
    (y2 + 2) = y2
because the equation was solved for (x1,y1)
so:
    x2 = x1 - 1
    y2 = y1 - 2
In a picture:



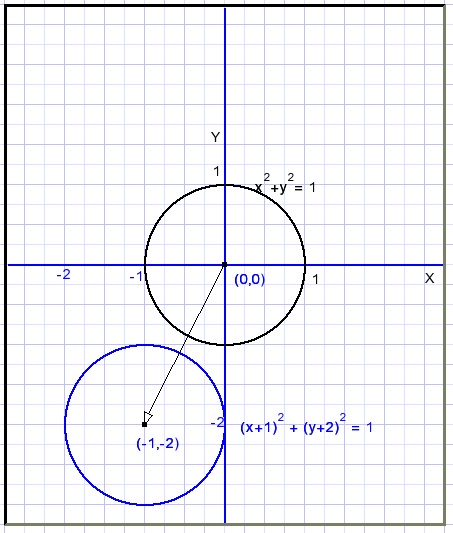
The graph is shifted 1 left and 2 down.
In general, if in any equation :
    x is replaced by (x+h) the graph will shift h positions left.
    y is replaced by (y+v) the graph will shift v positions down.

Note : For negative values of h and v the graph will shift right and up.

This is true for any function or equation.

Translation and equation
We start with circle x2+y2=1 and replace (x) by (x+h) and (y) by (y+v).
The result:
    (x+h)2 + (y+v)2=1
    x2+2hx+h2+y2+2vy+v2=1

The factors of the squares of a and b do not change.
New are terms with x and y showing up as 2hx and 2vy.
This indicates a translation.

Example
x2-10x+y2+6y=47 is a shifted circle.
    2h = -10.....h = -5.....shift of 5 to the right.
    2v = 6.......v = 3......shift of 3 down.

Scaling x,y

In equation x2+y2 = 1 we replace x by x/2.
What will happen?
Say (x1,y1) is on the circle and after the change this point has become (x2,y2).
This is true if:
    x2/2 = x1
    or
    x2 = 2x1


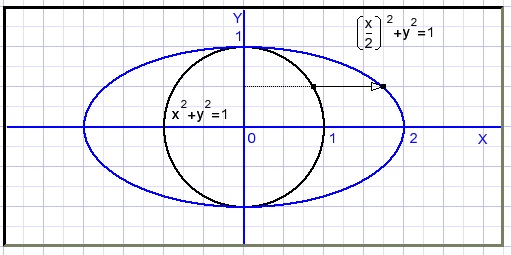
The result is doubling of the width.
Such a stretched (oval) circle is called an ellipse.

In general, if in any equation:
    x is replaced by (x/a) the graph will stretch by a factor a in horizontal direction.
    y is replaced by (y/b) the graph will stretch by a factor b in vertical direction.
Note: for factors < 1 the dimensions will shrink.

The general equation of an ellipse is:



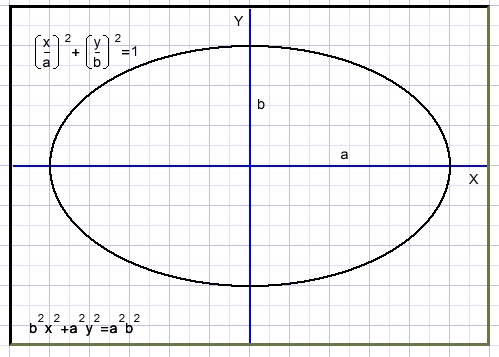
Scaling and the equation
Cicle x2 + y2 = 1 is stretched horizontally by a and vertically b resulting in (x/a)2 + (y/b)2 = 1.
Multiplication by a2b2 makes b2x2 + a2y2 = a2b2
Scaling changes the factors of the x, squares and the constant (without x or y)
No new terms with x, y are added.

Example
Given is ellipse 9x2+49y2 = 441.
Calculate "a" and "b".
Divide both terms by 441 :



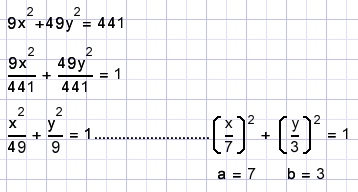
Rotation

We rotate point P(x1,y1) counterclockwise by angle φ
For convenience we observe x and y separately.



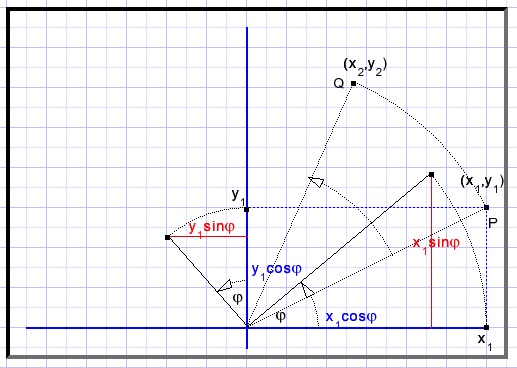
Q is the rotated point P.
The center of the rotation is origin (0,0).

Rotation of x1 causes
    x2 = x1cosφ
    Δy = x1sinφ.......infuence of x on y
Rotation of y1:
    y2 = y1cosφ
    Δx = y1sinφ........influence of y on x
Adding the results:
    x2 = x1cosφ - y1sinφ
    y2 = y1cosφ + x1sinφ
In general:
If in any equation with variables x and y :
    (x) is replaced by xcos(φ)-ysin(φ)
    (y) is replaced by ycos(φ+xsin(φ)
the graph will rotate φ degrees clockwise.
(Remember: the (x,y) values which originally solved the equation were located at counterclockwise rotation over degree φ)

Rotation and equation
Ellipse b2x2+a2y2 = a2b2 is rotated right by φ degrees.
The rotation center is (0,0).
The equation changes into
    b2(xcosφ - ysinφ)2 + a2(ycosφ + xsinφ)2 = a2b2.
Now write this equation without parentheses and terms with xy appear
    -2b2xysinφcosφ
    2a2xysinφcosφ
this is the way to recognize a rotation.
Rotation also changes the terms with x, y, x2, y2 and the constant term.

Example
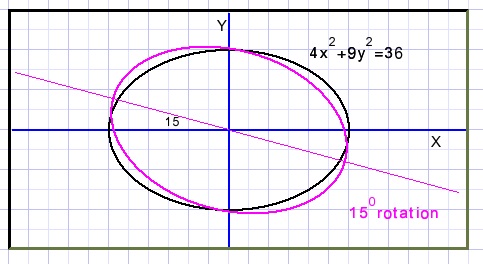
Ellipse 4x2 + 9y2 = 36 is rotated.
The new equation shows the term 2,5xy.
Question: over which angle did rotation take place?
    b = 2.
    a = 3.
    2(a2 - b2)sinφcosφ = 2,5
    10sinφcosφ = 2,5
    2sinφcosφ = 0,5
    sin(2φ) = 0,5
    φ = 15



Example
Given is ellipse: 2x2+y2 = 2(x + y + xy -1 ).
Below the graph is pictured:



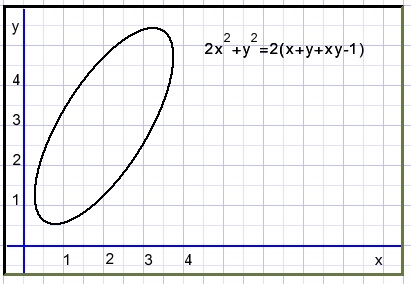
The x,y terms are the result of translation, the xy term indicates rotation.
How much?
First we try to shift the graph such that the x and y terms disappear.

replace x by (x+h) and y by (y+v).
This results in two equations which enables solving of h and v.
    2(x+h)2 + (y+v)2 = 2(x+h) + 2(x+v) +2(x+h)(y+v) -2
    Extract the terms with x and y :
    x terms: 4h = 2 + 2v
    y terms: 2v = 2 + 2h
    Simplify:
    2h - v = 1
    v - h = 1
    Solution:
    h = 2
    v = 3
This is in agreement with the graph.
The new equation becomes after shifting 2 left and 3 down:
    2(x+3)2 + (y+2)2 = 2[x+3 + y + 2 + (x+3)(y+2) - 1]
    after simplification:
    2x2 + y2 - 2xy = 3
Which rotation took place, which are the dimensions of the ellipse?

procedure to find the rotation
We depart from the general equation of an ellipse

However, right of the "=" character another number then 1 may be found.
This means that in fact a and b need to be changed.
Before we noticed that rotation changes a and b, no constant change.
In the equation b2x2 + a2y2 = a2b2 the number right of the "=" is the product of x2 and y2 factors.
Why is this important?
We see 2x2 + y2 - 2xy = 3
Right of the "=" is no 1 but a 3. Later I come back at this pitfall.

Say
    p = cosφ
    q = sinφ
then rotation of a graph over φ degrees clockwise takes place if
    (x) is replaced by (px - qy)
    (y) is replaced by (py + qx)
Now we apply this operation to the standard ellipse equation.
This results in a new equation with different factors of x2, y2 and xy terms.
Next we equate these values to those in 2x2 + y2 - 2xy.
This results in a new set of equations with a,b,p,q.
The goal is to solve these equations to know the rotation and a,b, the ellipse dimensions.

The calculated a,b where derived from an equation with format ....= 1.
However our equation shows ....= 3.
Therefore we depart from equation b2x2 + a2y2 = 3a2b2.
(from the form without denominators)



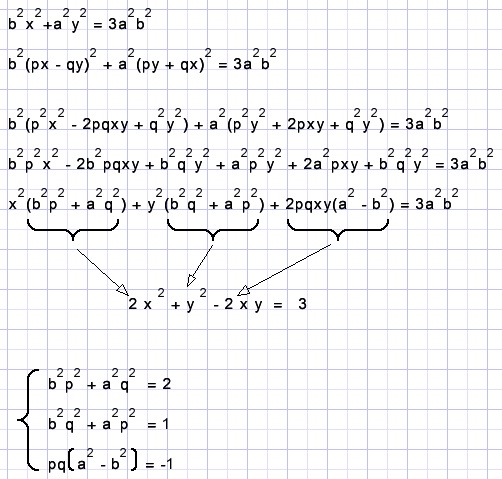
Above we see the set of equations to be solved.
p2 + q2 = 1 we could add.
First we look after p and q.
Subtract row 2 from row 1 and combine terms with p2 en q2:



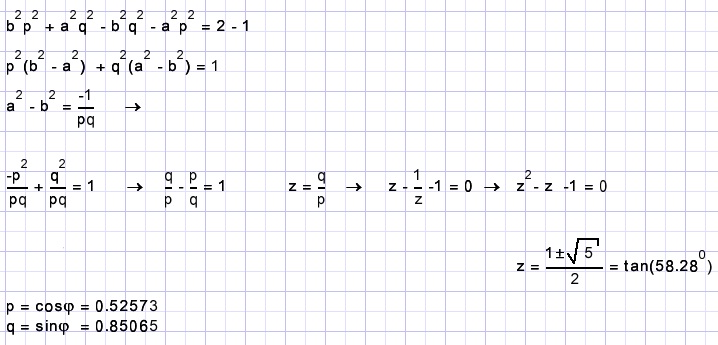
Note: φ is the angle of rotation. z = tanφ

Now we look after a and b.
Again the 3 previous equations with p,q,a,b are the start.
Add rows 1 and 2 and place p2 and q2 outside parenthesis:



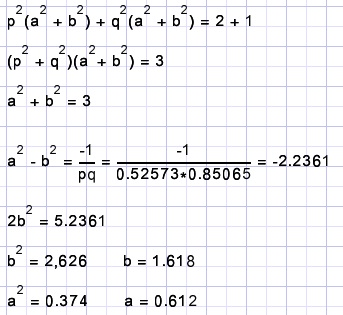
Right of the "=" comes 3a2b2 = 2,946.
The equation of the ellise was before translation and rotattion:



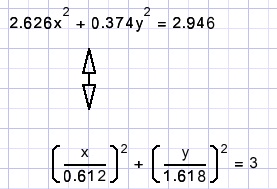
what the next picture shows:



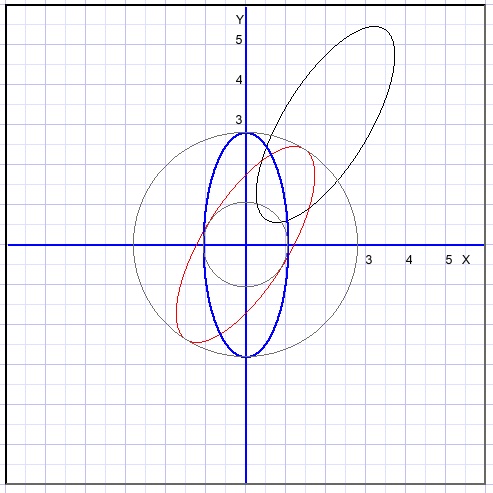
For clarity, two circles with radius a and b are included.

Exercises

We started this example with equation 2x2+y2 = 2(x + y + xy - 1)
But what about nx2+y2 = 2(x + y + xy - 1) for cases where n = 3,4,...
In a math Facebook group I found this problem:
solve the equation
    5x2+y2 = 2(x + y + xy - 1)
this seems a weird question at first glance because we see a shifted and rotated ellipse.
The plot of this equation however shows only one single point.
What happened? Which point?