A numeric calculation of π

download program
download Delphi(7) project



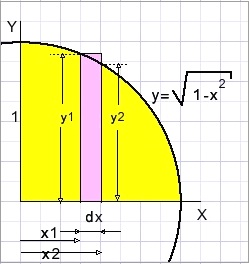
Area A of the total circle is πr2
With radius r=1 , A=π
Area A is obtained by cutting a quarter circle in vertical slices of width dx.
Then the areas of the slices are added.
Smaller slices, smaller dx, gives a more accurate result.
We add areas y1*dx (sum Aout) and also areas y2*dx (sum Ain).
The real area is somewhere between Ain and Aout.



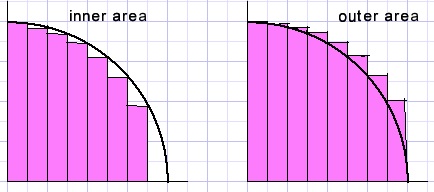
The choice of dx
Computers calculate in the binary number sysytem.
In this system, the value 0.1 can only be represented with a small error,just as 1/3 in the decimal number system.
Numbers of the format x/(2^n) are accurate (x, n are natural numbers).
Good values for dx are ½ ¼ 1/8 1/16 ….. etc.

The program



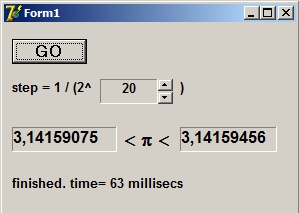
Step is dx.
An UpDown component selects the step value.
Both 4*Ain and 4*Aout areas are shown being the lower and upper boundaries of π.
The calculation is started by pressing the GO button:

procedure TForm1.Button1Click(Sender: TObject);
var dx : double;
    i : byte;
    Ain,Aout,x1,x2,y1,y2 : double;
    t1,t2 : longword;
begin
 label4.Caption := 'busy';
 statictext1.Caption := '';
 statictext2.Caption := '';
 application.ProcessMessages;
 t1 := gettickcount;
 dx := 1;
 for i := 1 to UpDown1.position do dx := dx *0.5;//make dx
 x1 := 0;
 y1 := 1;
 Ain := 0;   //inner area
 Aout := 0;  //outer area
 while x1 < 1 do
  begin
   x2 := x1+dx;
   y2 := sqrt(1-sqr(x2));
   Aout := Aout + dx*y1;
   Ain := Ain + dx*y2;
   x1 := x2;
   y1 := y2;
  end;
 Aout := Aout*4; //complete circle
 Ain := Ain*4;
 statictext1.Caption := formatfloat('0.00000000',Ain);
 statictext2.Caption := formatfloat('0.00000000',Aout);
 t2 := gettickcount;
 label4.Caption := 'finished. time= '+inttostr(t2-t1)+ ' millisecs';
end;
Select other values of dx to observe the differences in accuracy.