

| The theorems of Menelaus and Ceva |
Menelaus
Please see the following picture:Triangle ABC is intersected by a line in points P,Q,R:
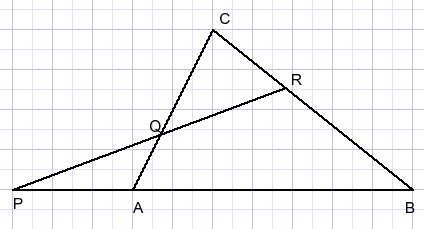
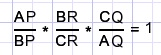
The theorem of Menelaus is:
Proof
Draw perpendicular lines : A-->A' B-->B' and C-->C'
This yields similar triangles AA'Q and CC'Q also CC'R and BB'R also AA'P and BB'P
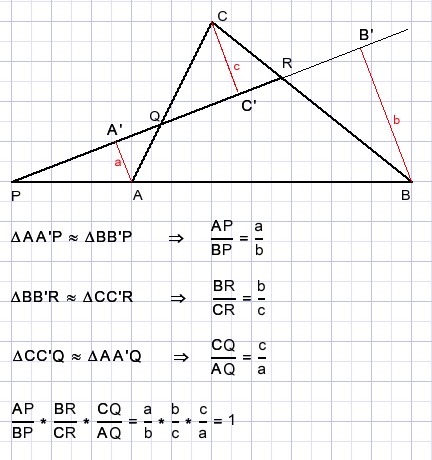
Inverse
If the product of line ratio's equals 1, the points P,Q,R are on a straight line.
The proof is not presented here.
Systematic approach
Starting at point A, walk over the triangle perimeter in counterclockwise direction.
So the path is AB, BC and CA.
In case of AB, write A. as numerator and B. as denominator of a fraction.
Repeat for BC and CA:

For A./B. substitute P for (.)
For B./C. substitute R for (.)
For C./A. substitute Q for (.)
Ceva

If three lines intersecting the angles of a triangle have a common point (S) then:
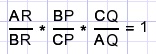
This is the theorem of Ceva.
Proof
We use the theorem of Menelaus.
Please look at ΔARC intersected by BQ and also observe ΔRBC intersected by AP.
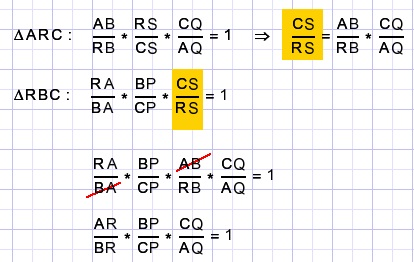
Inverse
If the product equals 1 the lines (crossing A,B,C) have a common point.
The sine rule of Ceva
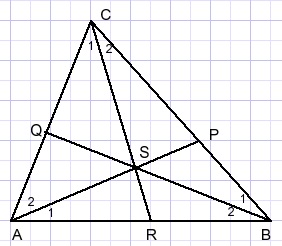
This rule is:
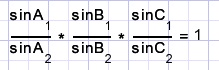
if intersecting lines (crossing A,B,C) have a common point (S).
Proof
Repeated application of the trigonometric sine rule in triangles ABS, BCS and ASC yields:
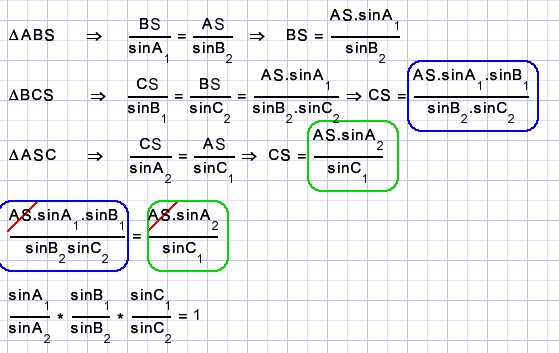
Inverse
If the above sine ratio's products are true, the lines through angles A,B,C intersect in one point.

