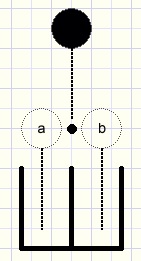
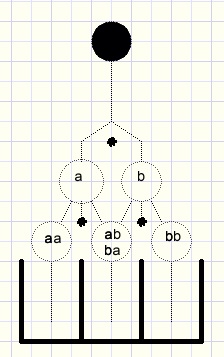
About Marble Boards and the Newton Binomium Below is pictured a marble board: fig1. A marble falls down, hits a nail and passes the nail either left or right. The left choice we call a the right choice b. Finally the marble falls in a bucket below. We add two more nails to the board and also a bucket: fig2. The marble ends in the left bucket if the choice was both times a (left). This path we call aa. The path for the right bucket is bb. Path ab (first left, then right) and also ba (first right then left) delivers the marble in the middle bucket. Choice a followed by b we write as the product ab. The choice of direction when a nail is encounterd we call a+b read: a or b. The left bucket may be called a2, the middle bucket ab + ba and the right bucket b2 Because in this case ab = ba the middel bucket may be called 2ab. Fig1. with 1 nail: (a + b)1 = a + b Fig2. : the marble passes two nails. The choice (a+b) must be made twice so the possible paths are: (a + b)(a + b) = (a + b)2 = aa + ab + ba + bb = a2 + 2ab + b2. 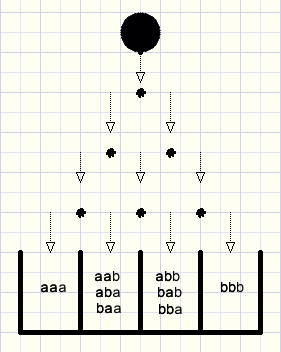Again we add more nails and a bucket: fig3. Now the marble has to make the (a+b) choice three times. (a + b)(a + b)(a + b) = (a + b)3 = aaa + aab + aba + baa + abb + bab + bba + bbb = a3 + 3a2b + 3ab2 + b3 a3 + 3a2b + 3ab2 + b3 may be written as: 1.a3 + 3.a2b + 3.ab2 + 1.b3 (point. means multiplication) One path exists to bucket a3. To buckets a2b and ab2 three paths exist in both cases and to bucket b3 only one path exists. In formula 1.a3 + 3.a2b + 3.ab2 + 1.b3 the numbers 1, 3, 3 and 1 are called the coefficients of a3, a2b, ab2 and b3. Gambling. We use our marble board of fig.3 to play this game: A visitor pays 1 dollar to drop a marble. In case the marble ends in the far left or far right bucket, we pay back 3 dollar. Will this game be profitable? The marble makes choice a or b three times so there are 2*2*2=8 paths which also is the sum of all coefficients 1 + 3 + 3 + 1. There are 2 paths to the left and the right bucket together. The probability for this left or right bucket is 2/8 = 25%. In 25% of the case we have to pay back 3 dollars. 1 - 0,25*3 = 25 cents, our average profit per game. We assume that the marble board was constructed in an honest way. Examples above may be extended with much more nails and buckets. In this case the calculation of the coefficients becomes a problem. Wouldn't there be a more simple method? The French mathematician Pascal (1623 - 1662) found one. Below is pictured his Pascal triangle in which each number is the sum of the two numbers just above. 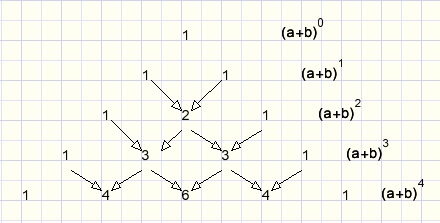fig4. We may read directly: (a+b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4. Each term has 4 factors holding the a and b choices in all possible combinations. This triangle was known centuries before by the Cinese. However also this triangle becomes a problem at very high powers. Is there a formula to calculate the coefficients directly? This question was also asked by the English fysicist and mathematician Newton (1643 - 1727) and he succeeded in finding it. The Newton binomium Please look at fig. 3 again. There exist 3 paths to bucket a2b : aab, aba, baa. The same amount of path as there are sequences of 2 characters a and 1 character b. Five characters a,b,c,d,e may be placed in 5*4*3*2*1 different sequences because: - for the first character there are 5 choices - for each next choice there is one less possibility. The product 5*4*3*2*1 we write shorter as 5! ...say "five faculty". 5! = 120 6! = 720 Five characters "a" only may have one sequence. However if we color them different there are 5! = 120 sequences. So, in case of 5 equal characters we have to divide by 5! , which is the number of sequences that are equal. Let's look at the middle bucket in fig. 4: 6.a2b2 The number of sequences of characters aabb is 6 (aabb,abab,abba,baab,baba,bbaa) In case of 4 different characters there would be 4! = 24 sequences but because of the 2 a's and 2 b's we twice have to divide by 2! = 2. 24/4 = 6 A more difficult example: We start with (a+b)10 = a10 + ....+ 120a7b3+ ...+ b10 Coefficient 120 is calculated : - there are 10 characters a and b together. If different there would be 10! sequences - there are 7 equal a's, so 10! must be divided by 7! - there are 3 equal b's, which means division by 3! 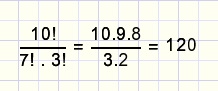fig5. 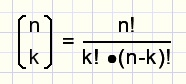This type of calculations show up a lot and a more compact notation was made: fig6. Say : n over k (do not draw line, this is no fraction) In fig 5. is: n=10 and k=7 Symmetry: n=10 and k=(10-7) have the same result. By definition: 0! = 1 Rule: (p+1)p! = (p+1)! 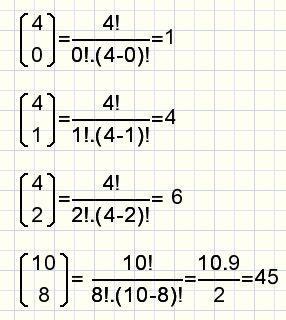Examples: fig7. 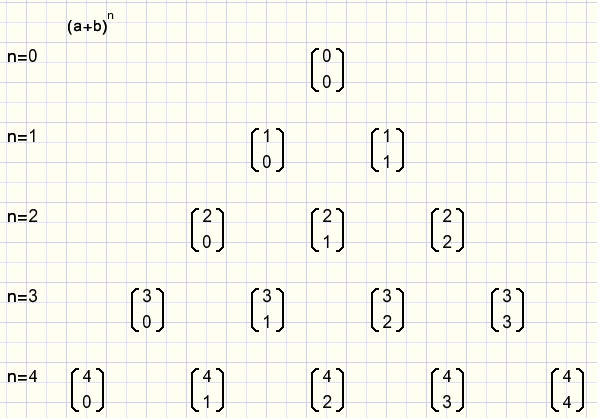Using this notation we may place the coefficients in a Pascal triangle: fig8. Now we may simply write: fig9. The notation can be even more compact by using the sum notation. This uses he Greek SIGMA sign to replace a sequence of + operators. 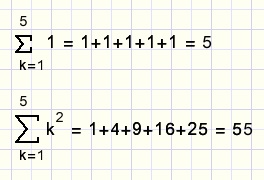Below are listed some examples using the sum notation: fig10. k is called the index. Below the sigma the begin value of the index is written. The highest index value is written on top of the sigma character. 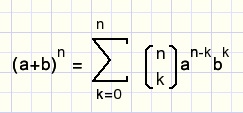Finally we have arrived at the Newton binomium fig11. Addition Please look at fig8. again. Look horizontally and also diagonally from left top to right bottom. 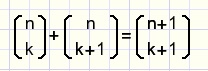Then we notice that this equation must be true: fig12. called the summing rule. A proof consists of writing each term as a coeffient followed by n over k then division by (n over k). 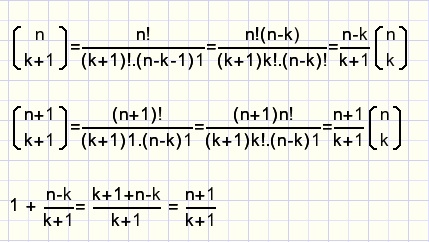fig13. Amazing, it's right ! 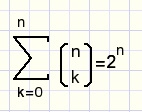Question Why is this true: fig14. Hint: which values of a and b were assumed? The Newton binomium has many applications in mathematics. Newton himself needed it to find the derivative of the function f(x) = xn. But also in combinatorics and probability calculations the binomium shows up. Example A group of 25 people travels in a tropical country. The probability that a person gets sick is 10%. So the probability nobody gets sick is 0,925 = 7,2% But what is the probability that just 5 people get sick? This problem resembles our marble board where a = 0,9 (not sick) and b = 0,1 (sick). With 25 a,b choices and outcome of 5 (k=5): fig15. Note: in case of the marble board we may write: a = 1/2 and b=1/2, the probabilities for the left or right path. Now each term of the binomoim is the probability that the marble ends in this particular bucket.