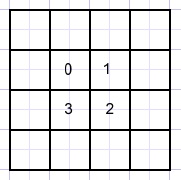
Magic squares (2) to 3x3 squares Also here we drop the requirement that all fields must have different numbers. We accept for now that only numbers are different per row, column, diagonal. Then the middle 4 fields must be 0,1,2,3 because they participate in a row, column and diagonal. There are many symmetries so the next digit placement is not important as long as the sum is 0+1+2+3=6. The 2*2 squares (left, right, top,bottom) must have 0,1,2,3 in their fields for the reason mentioned before. The other numbers follow. We notice that the same numbers often are a knight's move apart. 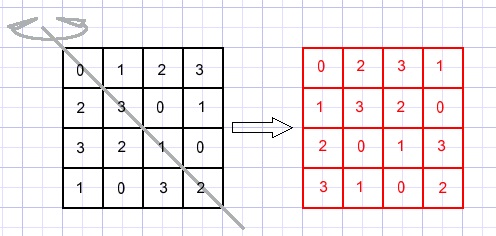Reflection around a vertical line does not work here because not all resulting numbers are unique. We try reflection around the left-top down diagonal. 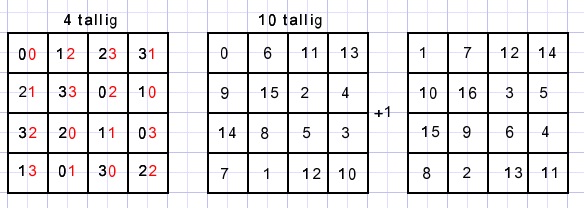Combining the fields, conversion from 4 to 10 based number system, adding 1 to each field: See ! Note that all 2x2 squares that hold a diagonal also yield a sum of 34. 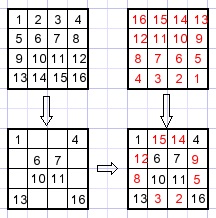A simple way exists to make magic squares that are a multiple of 4x4. Write the numbers 1,2,3.. in normal writing sequence. Also write these numbers in another square but in reverse order. In each 4x4 square erase the middle 2 fields of the 4 edges. Now take the corresponding numbers from the reverse square to fill the empty places.