Logic puzzle solving

The problem

5 persons : Mary, William, Peter, Ann and Rose,
5 tasks   : homework, examination, test, scription, paper
5 subject : language, math, geology, history, biology
5 ratings : 3,5,6,7 en 9

The conditions are:
1) The person making the scription had a higher score 
   than the person doing math, but a lower score than Rose.
2) Peter is not the person that did the homework.
   However he had a higher score than Ann, but a lower score than the person 
   doing history.
   Also we know that Peter did not score 4 or 6 points higher than 
   the person doing the examnination.
3) The girl doing the test had a higher score than Mary who did not do language
   but a lower score then the person doing biology.
4) William did geology and had a higher score than the person doing language.
   However his score was lower than the person making the paper.
----------------------------------------------------------------------------
Which task, subject and score belongs to which person?

Programming information

--------------------------------
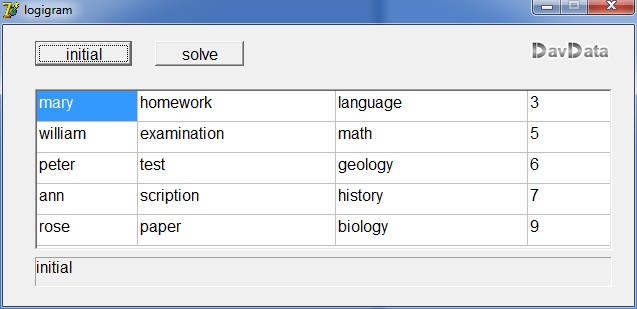
Below is the initial table to start with:
--------------------------------------------------------------
                             column                           |
--------------------------------------------------------------
0           1             2                   3               |
person |   task       |  subject        |   rating  |     row |
--------------------------------------------------------------
mary      homework       language             3     |      0  |
wiliam    examination    math                 5     |      1  |
peter     test           geology              6     |      2  |
ann       scription      history              7     |      3  |
roseie    paper          biology              9     |      4  |
--------------------------------------------------------------

While search for solutions, the persons in column 0 keep their position.
The rows in columns 1..3 however trade position until a good combination is found.

The tasks, subjects, persons and scores are denoted in the program by their 
row postion, so as 0,1,2,3 or 4.
The persons have the row number, as their postion is never changed.

Per column there are 5! = 120 sequences of tasks, subjects and scores.
A sequence is denoted by a number 0..119.
We need 3 of these numbers, which occupy array permNr[1..3].
(permutation is the math name for sequence)
PermNr[2] holds the permutation of column 2.

Above table holds permutation 0 of each column.

The numbers permutNr[1], permutNr[2] and permutNr[3] make a counter.
Each "number" counts 0..119, at 120 the counter overflows and a carry increases the 
next position.
PermutNr[1] being 120 resets itself to zero and increases PermutNr[2], etcetera.
In this way, all possible sequences are generated in an orderly way.

The conversion of a sequnce number to the actual sequence is done in this way:
(say we want to calculate permutation number 88)

   make permutation 0 first which is 0 1 2 3 4
   divide 88 by 24 = 3  (88 div 24 = 3)    note: 24 = 4!
   take the third element out of the row , which is -3-
   the remainder of the division  88/24   = 16   (88 mod 24 = 16)
   Remove the 3 from the row, which now becomes 0 1 2 4 x
   divide by 16, 16 div 6 = 2
   Take the second element from the row, the -2-
   16 mod 6 = 4   note: 6 = 3!
   Remove the 2 from the row, which becomes 0 1 4 x x
   4 div 2 = 2
   Take the second number out of the row, the -4-
   4 mod 2 = 0
   Remove 4 from the row, which becomes 0 1 x x x
   0 div 1 = 0
   Take number 0 from the row, which is the -0-
   The new row now is 1 x x x x
   Take the number left , the -1-
   Sequence number 88 is  3 2 4 0 1

Applying this sequence to the column "task" we get:

   scription
   test
   paper
   homework
   examination

Division by 24, 6, 3 and 1 is because of this reason:
there are 24 permutations of 4 elements. 
So they make a modulo 24 counter.
Therefore, the first 24 permutations will start with number -0-.
Permutations 24..47 will start with number -1- , etcetera.

Number div 24 gives the left most element.
This element must be removed from the list because we may not select it again.
Number mod 24 is de division remainder and with this number we continue.
Now, 4 more number must be selected.
The lowest 3 make a modulo 3! = 6 counter so the leftmost number 
is found by div 6.
remainder = remainder mod 6 is the number to continue with.
Selected numbers are removed.
Finally we add the number left.

To avoid making the same calculation all over again
a table is generated at create time : array permuts[0..4,0..119] of byte
holds 120 permutions (rows) 0f numbers 0,1,2,3,4.