

 | download Logic10 V2.0 |
Logic10: truth table reducer |
contents:
-
introduction
features
menu selections
installation
formula input
operations
table input
table output
reduction rules
CNF - DNF
inconcistent
tautology
save & load
translate information
scan information
virtual terms at work
history
donations
Introduction
Logic10 is a program that:-
1. Generates Truth Tables from formula's in Boolean Algebra
2. Reduces Truth Tables by applying the rules of Boolean Algebra
Click [ HERE ] for the programming of Truth Table reduction.
Logic10 is a great help in the study of Boolean Algebra, the design of digital electronic circuitry
and proposition logic in general.
This is Logic10 version 2.0
It supersedes all previous versions.
This is how Logic10 looks at work:(reduced image)
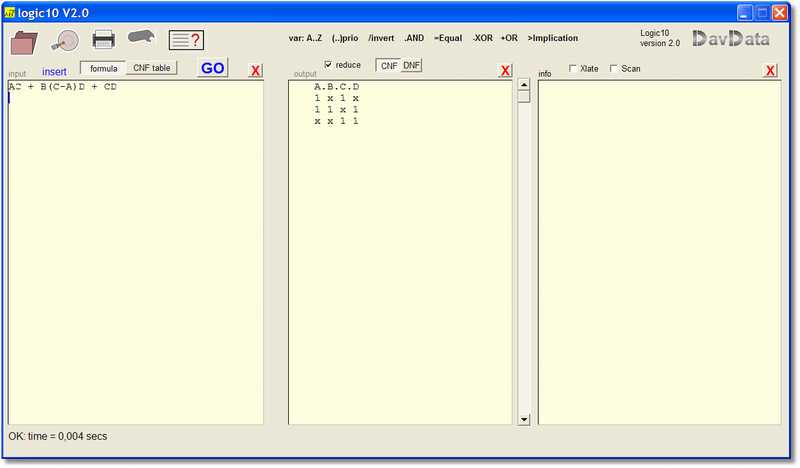
-
1. input and editing of formula's and truth tables
2. output of (reduced) truth tables
3. information about the formula translation or reduction process
Features
Logic10 features are:-
- input :(Proposition Logic) formula or Truth Table (CNF format)
- output : Truth Table in CNF or DNF format
- save and reload of all input and output data
- printing of input data and output results
- selectable: information of the formula translation process
- selectable: step by step information of the reduction process
- In-Line help information
Menu selections
see below:
The images left to right allow for
-
- opening a saved file (folder)
- storing truth table and settings to disk
- print input and truth table
- printer setup
- display help information
At the top of the output box, the choice between CNF or DNF output can be selected.
Also, a checkbox may be checked if the truth table must be reduced.
At the top of the Info box, two checkboxes may be checked:
one to display information of the formula translation and another to display information
about the truth table reduction steps.
Installation
Logic10 is written for Windows. The programming language is Delphi.Download Logic10 by clicking the download icon (lightning) at the top of this page.
There is no installation procedure, simply copy logic10 to a folder of choice.
The Windows registry is not changed.
Formula input
below is a detailed picture of the formula input box: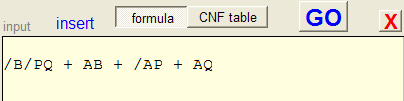
Logical variables are single characters A..Z
A choice of maximal 15 different characters is allowed.
Parenthesis (...) may be used 20 levels deep to prioritise operations.
Operators with their priority are
| operator | priority | name | description |
| / | 6 | NOT | Negation |
| . | 5 | AND | Logical Product |
| = | 4 | EQU | Equality |
| - | 3 | XOR | Logical Difference |
| + | 2 | OR | Logical Sum |
| > | 1 | IMP | Implication |
Notes:
1. between variables the "." AND operator may be omitted. The program adds the "." automatically.
2. the same between a variable and "(" or ") and a variable
3. also between ") .("
ABC = A.B.C
A(B+C) = A.(B+C)
(A+B)(C+D) + (A+B).(C+D)
Note:
In Boolean Algebra, negation (NOT) is normally indicated by a solid bar on top of the variable.
This is hard to edit on computer screens, so for Logic10 the "/" character is used just before the variable.
So ![]() is written as /A and
is written as /A and ![]() is written as /(AB)
is written as /(AB)
Beware:
When continuing a formula at the next line, a "." operator is inserted between successive variables so this formula
A+B C+DIs interpreted as : A+B.C + D
To eliminate a line, type ctrl y
To insert an empty line, type ctrl n
Operations
Table below lists the truth tables for all operations| A | B | /A | A.B | A=B | A-B | A+B | A>B |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
Truth Table input
Input may be a truth table of 100 lines maximal.Start typing a variable name (A..Z) at the top of the table.
The input table is in CNF form so, each line represents an AND of it's variables, lines are ORed.
Enter a "0" if the negated variable must be true, enter a "1" if the variable must be true.
So this table
A B C D
0 1 1
1 1 0
Represents the formula: /A C D + A B /DTruth Table output
When pressing the GO button, the formula is translated into a list of basic operations in the order of their priority.Then a counter is started to generate all possible 0,1 states of the variables and the operations are performed.
For CNF mode: if the final result yields true, the values of the variables are added to the output truth table.
For DNF mode: if the result is false, then the variable values are copied to the output truth table.
Also the variables itself are listed inverted: a -0- is listed as -1- and vice versa.
The explanation is given later in this article.
Reduction Rules
If the reduce checkbox is checked, then Boolean Algebra rules are applied to reduce the output table.There is no difference between CNF and DNF mode.
The following rules are used in this reduction process:
-
1.....A + A = A
2.....A + AB =A
3.....A/B + AB = A
4.....A + /AB = A + B
5.....A /B + BC --> AC
Note, that a formula like A + A represents a structure,
it may appear as D/F + D/F or as PQ/(X+Y+Z) + PQ/(X+Y+Z)
also, a formula like A + /AB may appear as /(A+B+C)K + (A+B+C)K
and A/B + AB may show up as A/BC/D + A/BCD.
Rule 5. is the main change from previous level 1.2
It replaces old rules 5. and 6. and solves all known "leaks" in the reduction process.
In rule 5. AC is called a virtual term and is only temporary added to the reduction process.
Rule 5. means, that if AC =1 then A/B + BC = 1, however the opposite is not true.
The terms A/B and BC are called the parents of AC
Reduction rules for virtual terms are the same as for normal terms with one exception:
-
a virtual term may not delete it's parent
The term itself is removed from the final truth table.
Adding the term without parents would change the formula.
A virtual- and normal term from the truth table may be combined (OR'ed) which may result in
-
- a new virtual term, which is saved in a stack for later processing
- reduction of the virtual term
- reduction or deletion of the truth table term
Virtual terms originating from other virtual terms also have more than two parents.
Parents are all terms that have contributed to a virtual term, either by reduction or generation.
Truth Table input
When pressing GO the input truth table is copied to the output table.If reduce is checked the table is reduced using above rules 1..5.
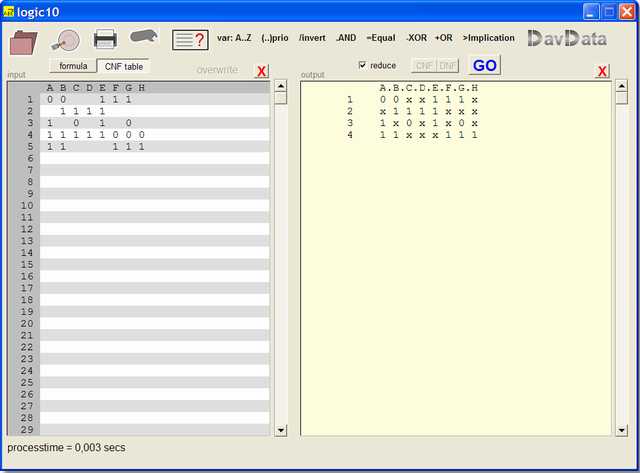
CNF and DNF
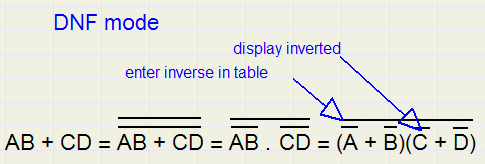
The output Truth Table may be in CNF or DNF form.CNF means "conjunctive normal form" which is ABC + DEF + GHI + .....
so, AND's of individual variables (with or without preceeding / ) which are ORed.
DNF means "disjunctive normal form" which is ( A+B+C)(D+E+F)(G+H+I)(....
so, OR's of individual variables (with or without preceeding / ) which are ANDed.
In DNF mode, when generating the output truth table, Logic10 enters variable values to the table for values
that generate false results.
Then the table may be reduced using the same rules as in CNF mode, but the table is listed in negated form.
A "0" is displayed as "1" and a "1" is displayed as "0".
Note: cnf..........AB + BC = (A+C)(A+D)(B+C)(B+D)..........dnf
This is a direct result of the second distributive law. (see Boolean Algebra tutorial)
Also the laws of de Morgan illustrate the relation between CNF and DNF
Inconsistent
A logic formula (proposition) is inconsistent if it never produces true.A simple inconsistency is:......A./A
Logic10 reports inconsistencies.
Tautology
A logic formula (proposition) is called a tautology if it is always true.A simple tautology is:........A + /A
Logic10 reports tautologies.
Save and Load
When clicking the save icon (disk platter) , a dialog window is opened to select the filename.Logic10 uses no filename extensions, as there are allready enough of them.
However, for clearity, the selected filename is prefixed by logic10_ (if not already).
All data: input formula, input CNF table and output Truth Table are saved in one file.
To reload saved data, click the map icon and select the file.
Translate information
if the xlate checkbox is checked, information about the formula translation is displayed in the info box.below is a detailed picture
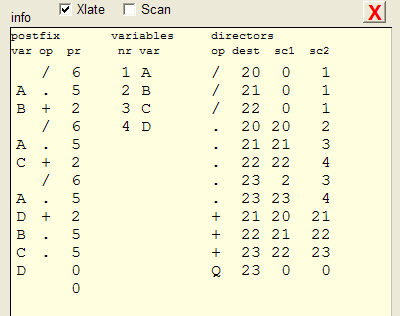
A third column with the priority of the operation is added.
From this table, the variables table is made.
The right director table is the final result of the translation.
It holds all operations sorted on priority level.
It has 4 columns:
-
1. the operation
2. the destination register
3. source operand1 register
4. source operand2 register
By setting the variables to specific values and executing the director table, the formula is evaluated true or false.
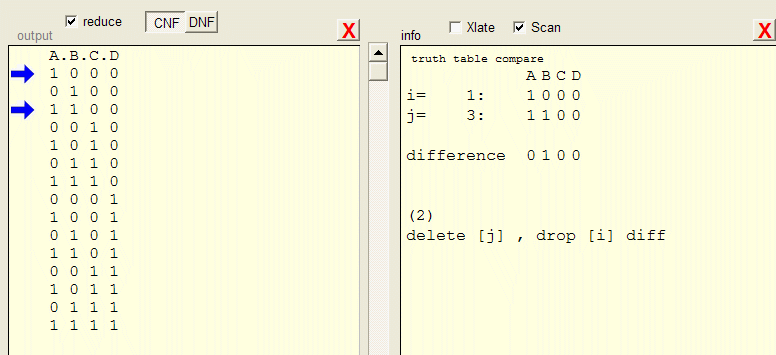
Scan information
Scanning the truth table amounts to comparing (ORing) each row ( term) of anded variables with every other term.Index to the truth table are [ i ] and [ j ].
So, truth table entry [ i ] is compared to entry [ j ].
Analyses of a pair of terms yields 4 boolean results:
hi
Hole-iThis is true when [ i ] has deleted variables that are present in [ j ]
A B C D E F
[i] 0 0 x 0 x x
[j] 1 0 x 1 1 0
In the table above, E, F variables are eliminated in [ i ] but not in j, so hi is true.hj
Hole-jThis is true when [ j ] has deleted variables which are present in [ i ]
A B C D E F
[i] 1 x 1 1 0 0
[j] 0 x 0 x x x
Here [ j ] has deleted variables D,E,F that are not deleted in [ i ], so hj is true.sb
Single bit means that the difference (exclusive or) of [ i ] and [ j ] only has 1 bit set.
A B C D E F
[i] x 1 1 1 0 1
[j] 0 x 1 1 1 1
Only the E bits are different. Columns having an x (deleted variable) are ignored.So, sb is true.
zb
Zero result, also called equal or no difference
A B C D E F
[i] 0 1 1 1 x 0
[j] 0 1 x 1 1 0
Columns with x are ignored.The other columns must be equal.
So, zb is true.
hi(3) hj(2) sb(1) zb(0) are bits 3,2,1,0 in a code.
This code selects the proper logic operations on [ i ] and/or [ j ] to reduce the truth table.
Some examples:
Reduction rule 1
AB/C + AB/C = AB/C
A B C
[i] 1 1 0
[j] 1 1 0
The difference is 0 0 0.hi, hj, sb are false (0), zb is true (1).
Action code = 1.
So, the [ j ] term is deleted.
Reduction rule 2
AB + ABC/D = AB
A B C D
[i] 0 1 x x
[j] 0 1 1 0
hi is true, hj is false, sb is false, zb is true.Action code is 1001 = 9 (decimal).
[ j ] is deleted.
Reduction rule 3
A/BC + ABC = A
A B C D E F
[i] 1 0 1 x x x
[j] 1 1 1 x x x
hi,hj,zb are false. sb is true (B is different only).Action code is 2.
The B variable in [i] is deleted, all variables of [ j ] are eliminated.
Reduction rule 4
AB + A/BC = AB + AC
A B C
[i] 1 1 x
[j] 1 0 1
hi , sb are true. zb, hj are false.The difference bit B is eliminated in [ j ].
Reduction rule 5, virtual terms
AB + /BC ---> AC where AC is a virtual term, used only for scanning.
A B C
[i] 1 1 x
[j] x 0 1
hi,hj,sb are true. zb is false.
Action code 1110 = 14 decimal.Action :
A scan is started to compare virtual term AC with every term in the truth table.
Rules 1..4 apply with the only restriction that [i] or [j] may not be deleted because they are parents.
Below is typical info of a normal scan
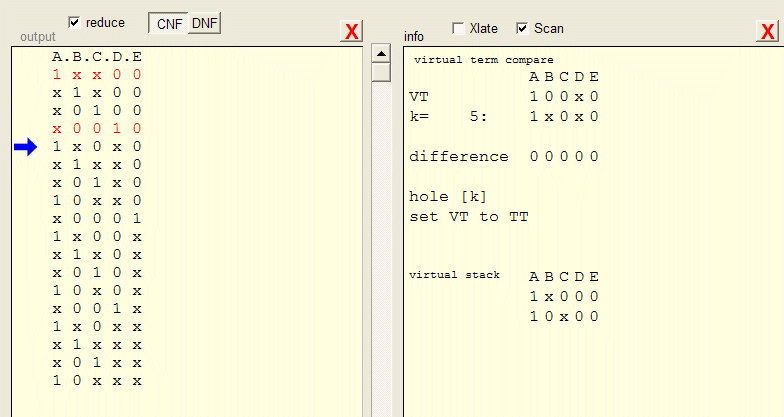
k is index in the truth table ( as i , j are for the normal scan)
A virtual term may (compared with truth table terms) generate new virtual terms.
These terms are stored in a stack (actually FIFO buffer) to be processed later.
In the truth table, the parent terms of the virtual term are listed in red.
Virtual terms at work
The introduction of virtual terms eliminates all former extra rules beyond 1..4First let me explain how the idea of virtual terms came up.
Formula /BQ + /AP + AB input resulted in /B/PQ + AB + /AP + AQ
This result is not wrong, but the term listed fat is redundant ( as is /P in /B/PQ)
The first idea was to find a method to eliminate the extra term AQ, but a second idea came up:
how to make use of it .
It appeared that AQ resulted from /BQ + AB, terms being different for B only.
So, AQ represents /BQ + AB. If AQ = 1 then sure also /BQ + AB = 1 (but not the opposite).
AQ may be temporary added as a term to force reduction in other terms and even be reduced itself.
In this case, terms /BQ + AB make virtual term AQ.
Then comparing AQ with all other entries in the truth table finds another AQ and eliminates it according to rule 1.
Example 1: /AZ + /BZ + /CZ + ABC = Z + ABC
/AZ + ABC ----> BCZ (virtual)
BCZ + /BZ = CZ (virtual term reduced) + /BZ
CZ + /CZ = Z + Z ...........and rules 1..4 can finish the job.
Example 2: BC + /BP + ACPQ = BC + /BP
BC + /BP ----> CP (virtual)
CP + ACPQ = CP........so ACPQ is eliminated.
Example 3: /B/PQ + AB + /AP + AQ................{see above}
/AP + AQ ---> PQ (virtual)
PQ + /B/PQ = /BQ + PQ.......variable /P is eliminated.
/BQ + AB ---> AQ (virtual), which eliminates other term AQ in the truth table.
History
The first version of this truth table generator/reducer I wrote in 1991 during my math study.A 10 (highest score) was offered to each student who could write a program to diagnose a
proposition logic formula as "inconsistent" or "tautology".
I wrote the program in Turbo Pascal (under MSDOS) and gained the "10".
Januari 2013, when cleaning my room, I found the old diskette.
It appeared that the program worked fine in spite of the old-fashioned user interface, but some tables
where not reduced to the limit.
Only reduction rules 1..4 were applied.
I started to work on it again.
The result was Logic10 version 1.2 in which 2 new rules were added
-
1. A/B + A/C + A/D + BCD = A + BCD
2. AB + /BC + AC = AB + /BC
However, still some cases remained were reduction was not to the limit.
Version 2.0 , with virtual terms, together with reduction rules 1..4 cleans up every truth table.
Finally.
Donations
Logic10 is freeware.In case you make commercial use of Logic10, consider a donation.
Please send me a mail for details.

