Hanging cables

Problem

A non-elastic but flexible cable of a fixed length is attached at two points.
Which function describes the points on such an arc?
This article explains.

Given are the length L of the cable and the coordinates of the two ends: (x1,y1) and (x2,y2)

The basics

For a proof of the next functions please refer to Wikipedia, using "catenary" or "hanging cables" as keywords.
The general function describing the hanging cable arc is
    y = a.cosh(x/a).....................where cosh(x) = (ex+e-x)/2
The length L1 of an arc from x=0 to x = x1 is
    L1=a.sinh(x1/a).....................where sinh(x)=(ex-e-x)/2
The next pictures presents some arcs for different values of a:



We notice that the vertex is positioned on the Y-axis, which also is a line of symmetry.
A is the scaling factor, both horizontally and vertically.

For a start, our problem is this:



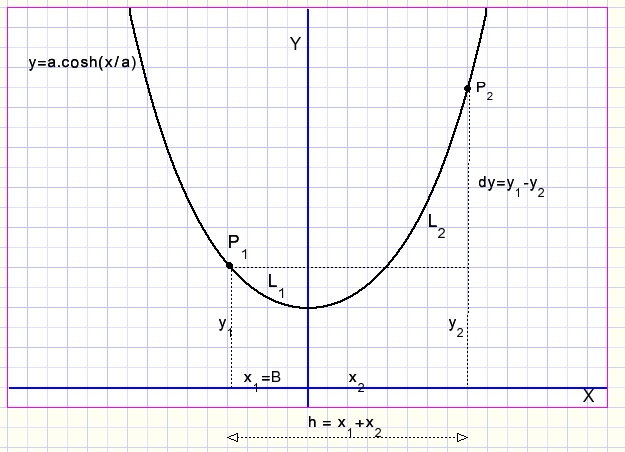
Known values are the coordinates of points P1 and P2 and h = x1+x2
In this graph the minimum is y=a, but by adding a value C the function is shifted vertically without a change of L.

So what matters right now is the cable length L=L1+L2,
the difference dy = y2-y1 and the horizontal distance h=x1+x2.

This is what we know:



First we want to know a.
We need to eliminate x1, x2, y1, y2 replacing them by the known values L, h and dy.

The calculation of a




Now we apply the rule:



and continue:



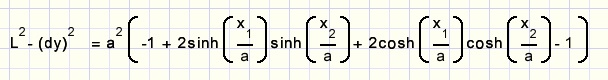
Next we apply the rules:



and continue:



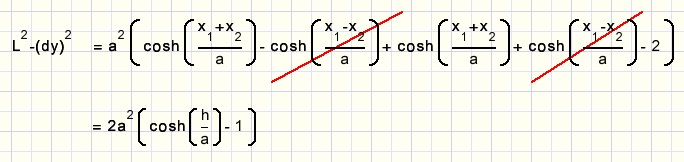
One extra step by applying this rule:



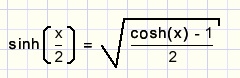
and finally we arrive at:



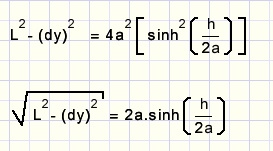
In this equition a has to be solved numerically.

Calculation of b=x1

Knowing a, b=x1 may be calculated.

We apply the rule:



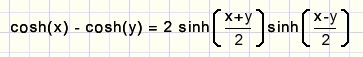
and continue:



In the final formula we want P1 on the Y-axis, so b = x1 is the horizontal shift required.
Note: this is done by replacing x by (x-b).
After this shift x1 = 0, x2 = h.
So far we have only used dy, not y1 and y2.
The minimum of the curve is a above the X-axis.

To make the curve hit points P1 and P2 a vertical shift is required.
Final formula:



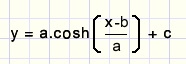
Calculation of c


Knowing a,b and y1 directly calculates c:



Delphi program

In this program h (horizontal distance of points) = 20. 
procedure calculateArc(var A,B,C : double; y1,y2: double);
//given: linelength, (0,y1) , (20,y2)
//calculate formula y = A*cosh((x-B)/A) + C
var a1,a2,QLV,V,dy : double;
begin
 a1 := 1;
 a2 := 100;
 dy := y1-y2;
 QLV := 0.5*sqrt(sqr(linelength)-sqr(dy));
 repeat
  A := 0.5*(a1+a2);
  V := A*sinh(10/A);
  if V > QLV then a1 := A;
  if V < QLV then a2 := A;
 until abs(QLV - V) < 0.0001;
 B := A*arcsinh(dy/(2*A*sinh(10/A))) + 10;
 C := y1 - A*cosh(B/A);
end;
a is solved numerically by clamping between a1 and a2.
Note: the uses clause must include "math".

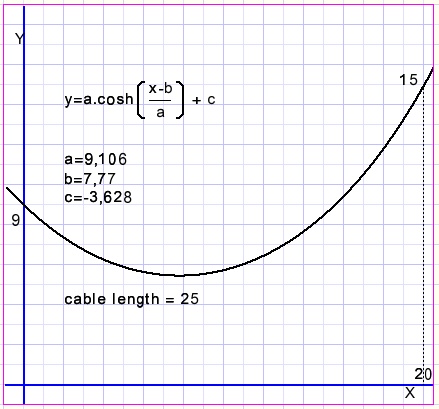
An example to end this article: