The grazing goat problem

Two farmers together own a circle shaped meadow.
One farmer lets his goat graze.
The animal is attached to a line which is pinned in the ground somewhere at the border of the land.
The meadow's radius is R.
Question: what is the length of the line allowing the goat to graze just 50% of the land?



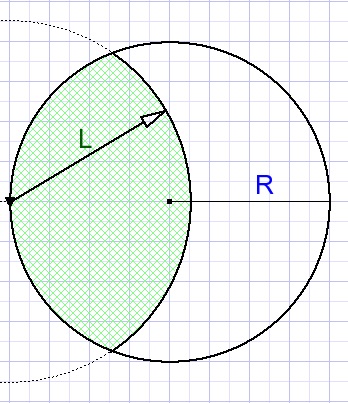
Moving from agriculture to college we notice overlapping circles.
The biggest circle with radius L (the rope attached to the goat) and the other circle (grassland) with radius R.
The distance of the circle centers is R.

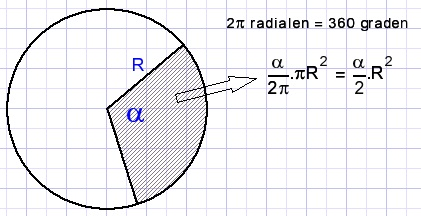
The area A of a circle having radius R is A = πR2.
The area of a segment with angle α is (α/2)R2
where angle α is measured in radians.
Note:
Radians are the lengths of arcs.
Angles are measured as arc length of a circle with a radius of 1.
A full circle is 2π in length.



What area has the circles overlap?
This is not obvious at first glance so we go step by step.



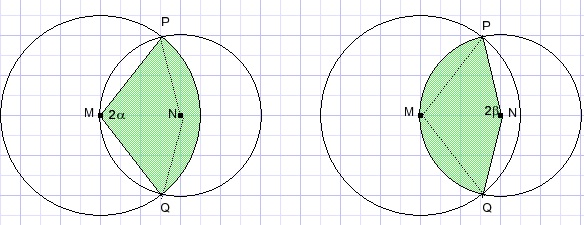
First the segment of the left circle with center M.
Next the segment from center N of the right circle.
Adding these segments includes counting quadrilateral PMQN twice.
So, this value has to be subtracted.
The area of half of the grassland is (π/2)R2 so now we may write the equation:



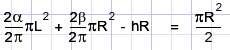
Here hR is the area of quadrilateral PMQN.
R = MN, h is the distance from P to MN.

Simplifying the equation:



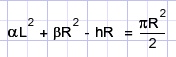
R is a known value.
Knowing angle α , β , h and L can be calculated.
See the figure below which also makes clear why angles of 2α and 2β were choosen.



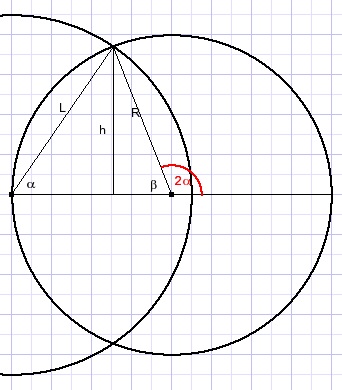
Starting with α we notice
    L = 2Rcos(α)
    h = Rsin(β)
    β = π - 2α
substitution in the previous equation:



Note:
we applied this rule:
    2cos2(α)-1 = cos(2α)
true because:
    1. sin2(α) + cos2(α) = 1
    2. cos2(α) - sin2(α) = cos(2α)
Add lines ..1) and ..2, voilą.

The next step is solving the last equation in the previous figure.
There is no rule for equations of this type.
One method is successive approximation (trial and error).
However much faster is the use of an equation plotter and simply reading the result.

Graphics-Explorer is such a plotter.
Be sure radians are selected.
Enter these functions (select different colors per function)
    y = sin(x) - x*cos(x)
    y = p/2
Note: p stands for π

then zoom in to the intersection.
We read x = 1,906,
α = 1,906 * 0,5 = 0,953....radians
cos(α) = 0,5792

The goat must have a line of length L = 2Rcos(α) so:

L = 1,158R

The angle α is in degrees: 0,953*180/π = 54,6