| A difficult geometry problem |
Request
Below I publish solutions of a geometry problem.You will find analytical (numeric), trigometrical but no geometrical solutions.
In case you have a new approach to this problem please let me know.
Your work will be published here.
Thanks in advance!
Problem

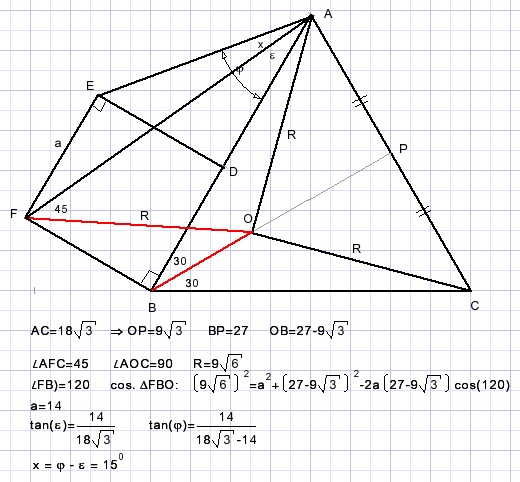
Above is pictured an equilateral triangle ABC and square ADEF.
LBFC=45o.
Proof that LECF=15o deg.
How to construct this figure?
-
- point G is the center of AB.
- extend edge BA.
- rotate GC 90o counterclockwise.
- HG=GC.
- construct circle through points H, B, C.
- F on circle such, that LHAF=30o so, AF perpendicular to AC.
- rotate AF clockwise, intersection with AC is point D.
- rotate AF around centers F and D, intersection is point E.

LCHB = LCFB so are on circle.
Let AF=2 and AB=2p.
Given LBFC=45o enables calculation of p.
Knowing p, the coordinates of points C,E,F can be calculated.
Then Lx (LECF) may be calculated.
For these calculations using complex numbers is convenient.
Calculation of p

Point A is designated as (0,0).
Coordinates of other points follow easily.
Multiply EB by (1+i) which caused 45 degrees ratation.
The product vector has the same argument as vector EC.

Lx = LECD is the difference of vectors CE and CD.
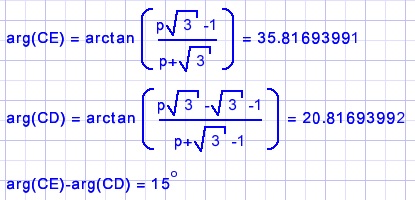
Lx=LDCE=15o
Request for help
Problem posted in Facebook group "Classical Mathematics" of Omid Motahed.Below I publish the responses.
Response (1)
Dejan Piscevic.He applies the sine rule in three triangles to obtain 3 equations with unknowns x, b and z.
Presents solution x=150 but no calculations are included.
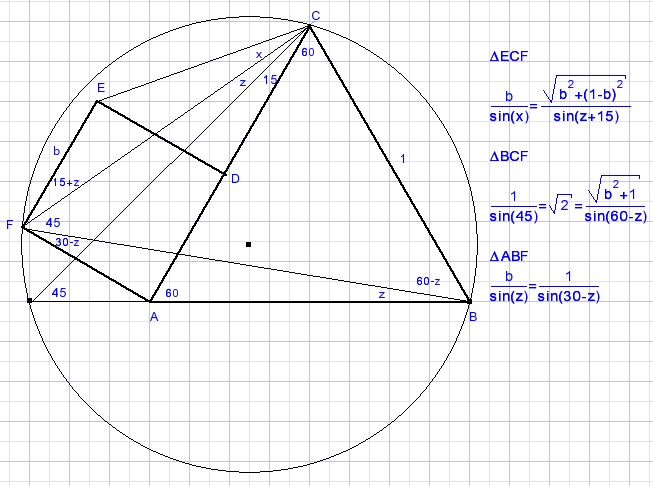
I continue
See figure above for the calculation of b.

Unclear is yet if Lx exactly is 150.
Not rounding the roots in the formulas for b and tan(x) may answer this question.
Construct equilateral triangle AMD, M on AB.
Draw circle with center M through points E and F.
Next, prove that point C is on this circle:
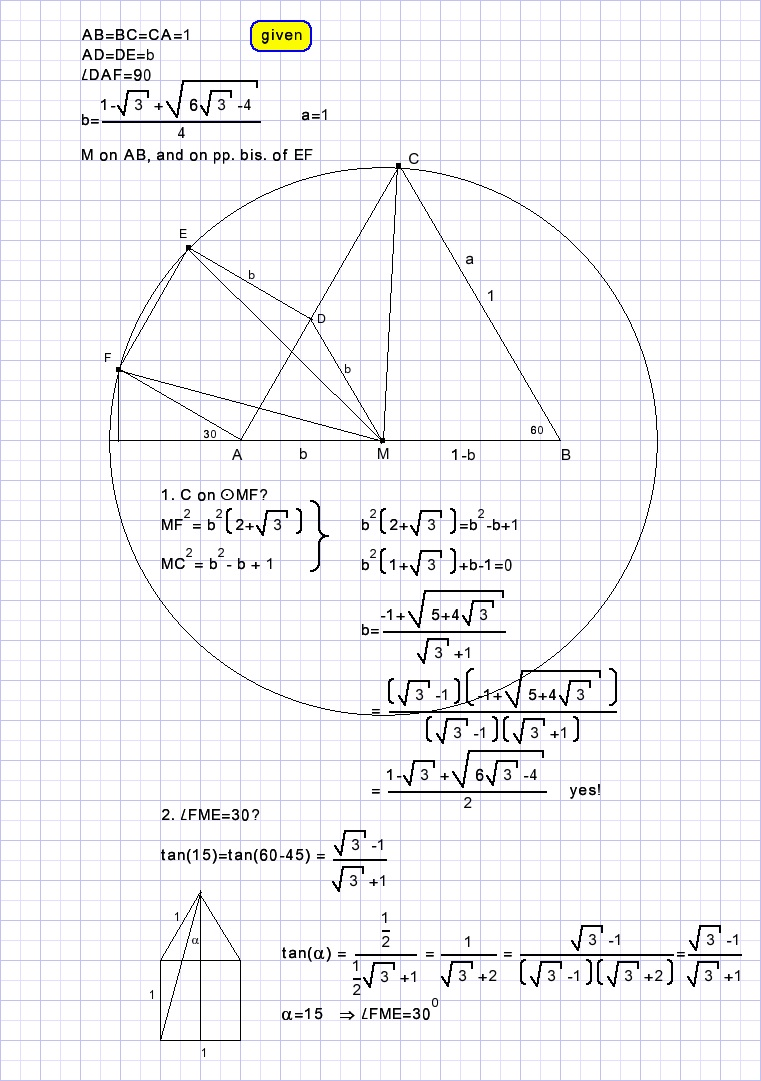
LECF spans arc EF so Lx = 30/2 = 150.
Response (2)
Wong Sii Hiang: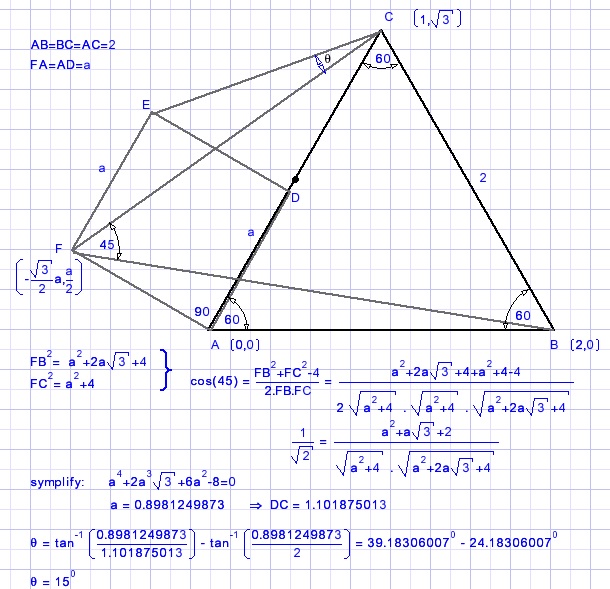
Response (3)
Hans Karl Abele: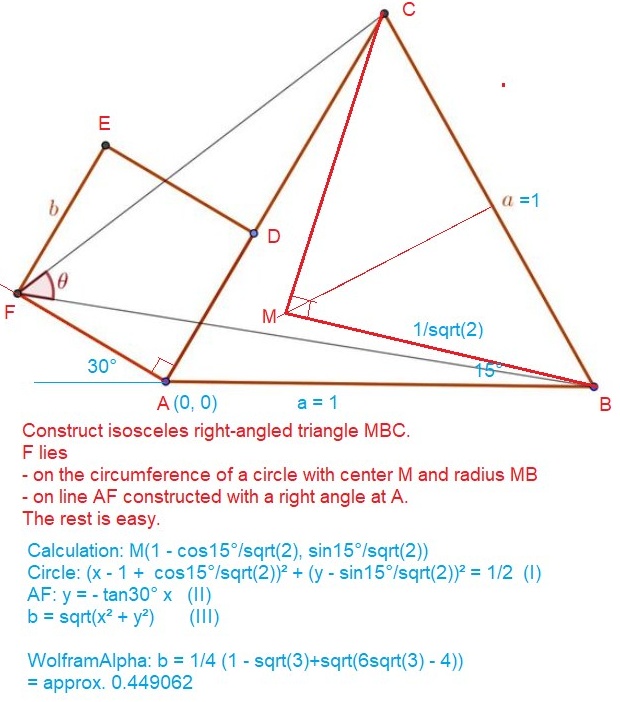
Response (4)
Biro Istvan :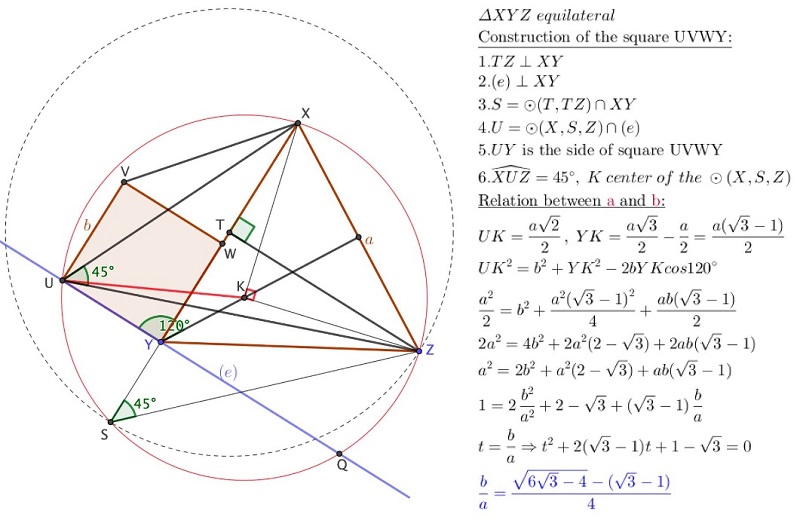
Response (5)
Viktor Martoni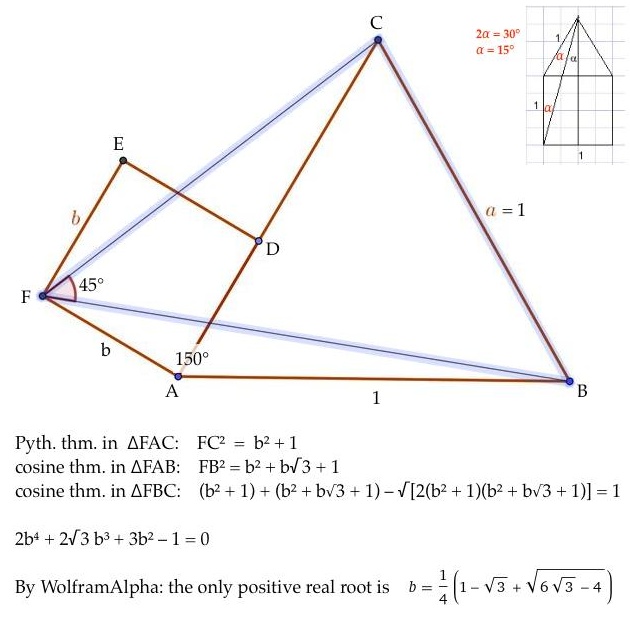
Response (6)
Joszef Nagy Vonnak