

| Geometry and statics |
The rules of statics may be applied to plane geometry.
See balance below:
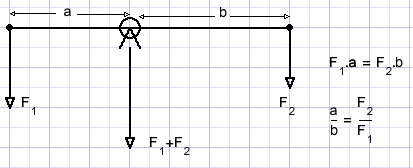
Example 1
The medians in a triangle divide each other in a ratio of 2:1, counted from the angle.
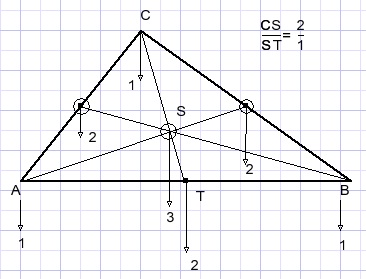
Apply a force of 1 in A.
The force in C also is 1, because of the medians.
Etc.
So, CS.1 = ST.2.
This is a special case of a general rule.
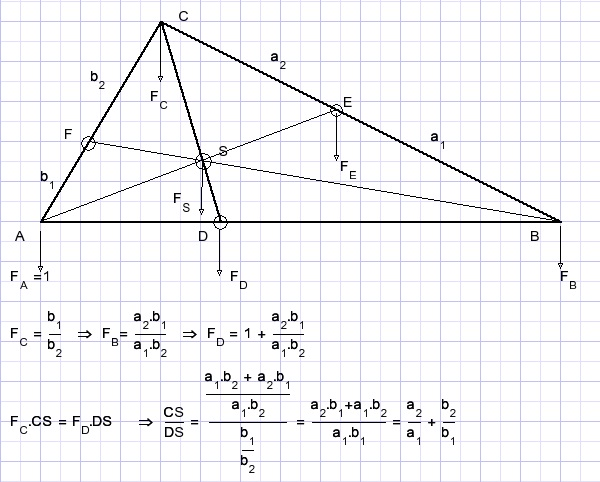
Example 2
A problem: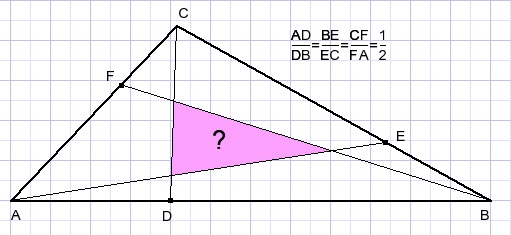
Which part of the triangle is the colored area?
Because of the symmetry we notice:
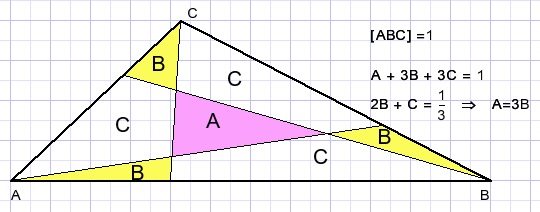
Which part of the traingle is area B?
We apply the rule:
-
If triangles share an angle, their areas have the ratio of the product of the edges around the angle.

The proof is left to the reader.
Back to the problem.
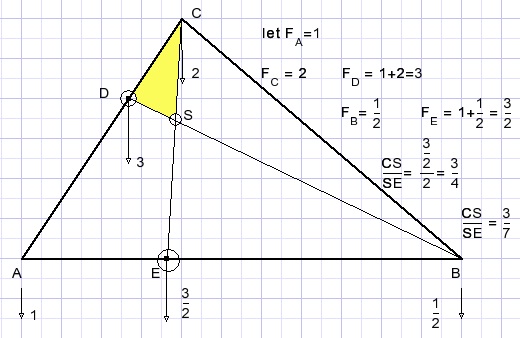
So, the yellow area = (3/7).(1/3).[CAE] = (1/7).[CAE].
[CAE] = (1/3).[CAB].
[CDS]=[1/21].[CAB].
Purple colored triangle = 3.[CDS] = (1/7) of triangle ABC.

