

| Geometry problem answers6 (50..59) |
50.
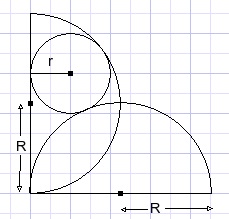
| calculate the ratio |
Solution

51.
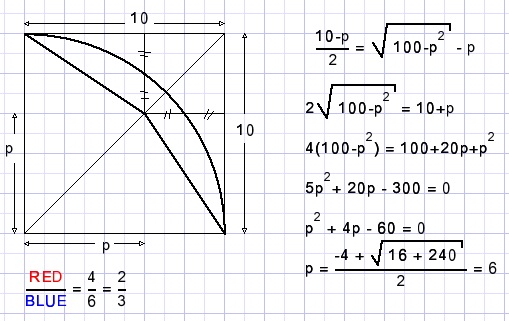
Below is pictured a square and a quarter arc.
Calculate the ratio of the blue and red areas.
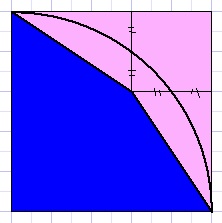
Solution
52.
Below is pictured a slightly overturned rectangle.
Prove that the colored areas are equal.
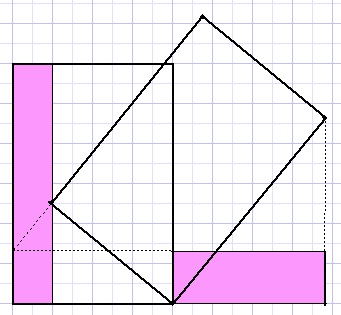
Solution
53.
Calculate the area of square ABCD.

Solution

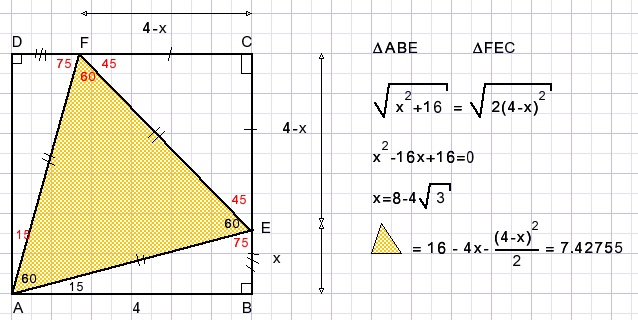
54.
AB=4.
Calculate the area of the colored triangle.
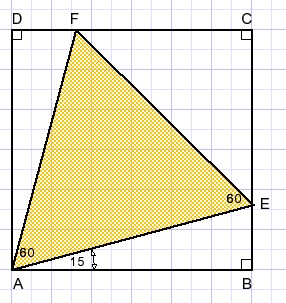
Solution
Triangles ABE and ADF are congruent (case edge,angle,angle) so BE=FD , AB=AD.ABCD is a square.
Let BE=x.
Apply Pythagoras lemma:
55.
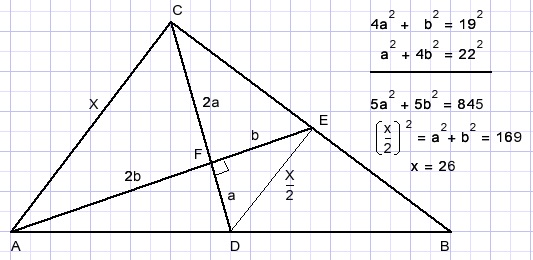
In picture below the medians are perpendicular.
Calculate side x.

Solution
The medians intersect at ratio 2:1 counted from the angle.Let DF=a, EF=b.
AD=22, EC=19.
Apply Pythagoras lemma:
56.
Calculate angle x in the circle arc.

Solution
Observe isosceles traingles.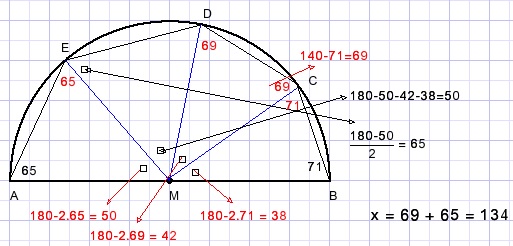
Sequence of calculations:
-
LMCB = LMBC = 71
LMCD = 140 - 71 = 69
LMDC = 69
LBMC = 180 - 2.71 = 38
LCMD = 180 - 2. 69 - 42
LAME = 180 - 2.65 = 50
LDME = 180 - 50 - 42 - 38 = 50
LMDE = (180 - 50)/2 = 65
x = 69 + 65 = 134
57.
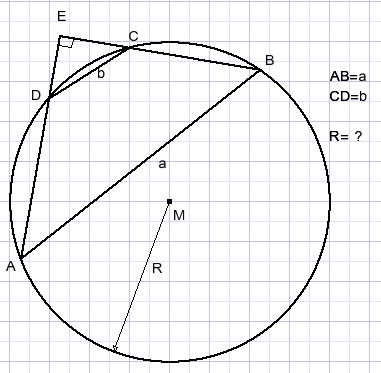
Solution
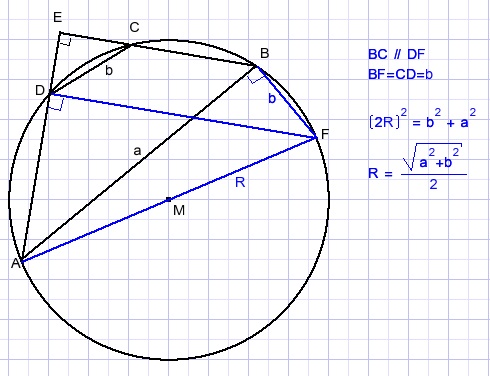
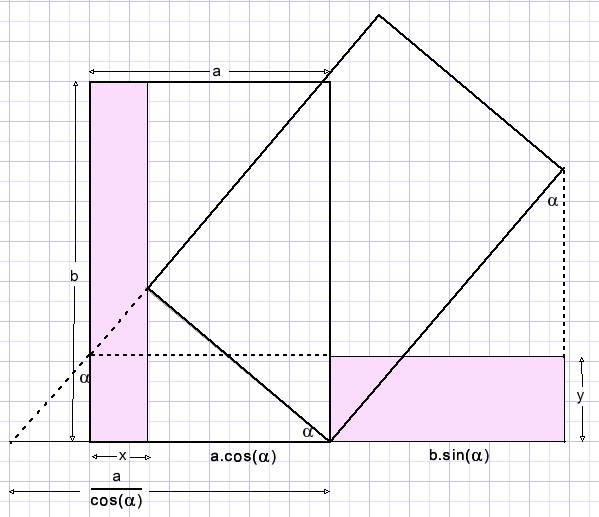
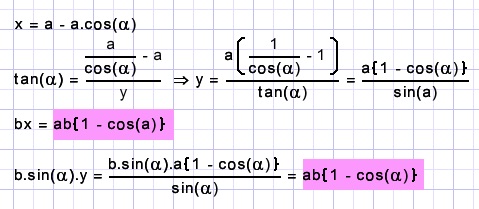
58.

The colored rectangles are identical.
a.
Calculated angle α
The area of a colored rectangle is 10.
b.
Calculate the area of rectangle ABCD.
Solution
a.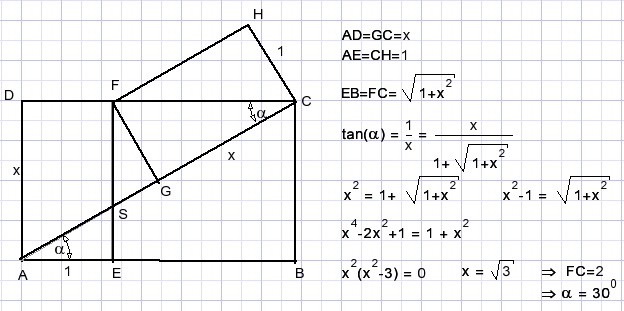
b.
[FGS]=[AES]
[ACD]=[FGC]+[AEFD]=10+5=15
[ABCD]=2.15=30
59.
Given is rectangle ABCD and a circle that contacts sides AB and AD.
C is on this circle.

Question: find f(x)= area of ABCD.
Solution


