Geometry problem solutions 5 (40..49)
40.


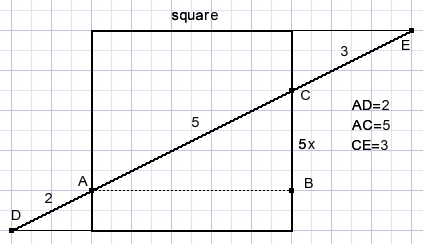
Calculate the area of the square.

Solution

Due to similarity of the triangles: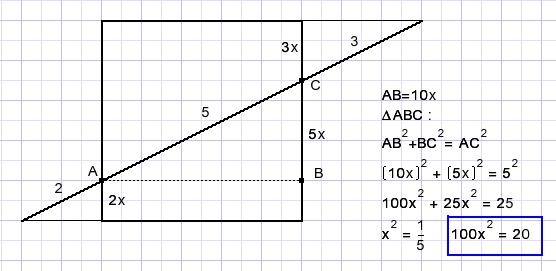


41.
Given is quadrilateral ABCD and some angles.
BC=DC.
Calculate angle x.



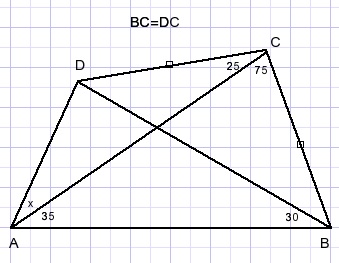
Solution




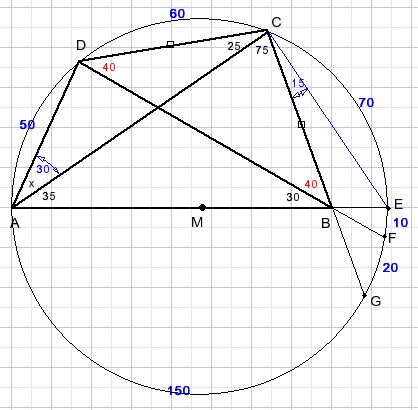
Draw circumscribed circle of ΔACD.
E is intersection of circle with extension of AB.
F is intersection of circle with extension of DB.
arc AD = 2*25 = 50.
arc AG = 2*75 = 150.
arc CE = 2*35 = 70.
LCDB = LDBC = (180-(25+75))/2 = 40.
arc CF = 2*40 = 80.

We notice that AE is the diameter of the circle. M is the center.
So:
LBCE = 90-75=15.
arc GE = 2*15 =30.
LABC = 70 = (arc AC + arc GE)/2.
arc AC = 110.
arc DC = 110-50 = 60.
x = 60/2 = 30 degrees.

Proof that AE is the diameter of the circle.
Draw lines MC and MG.



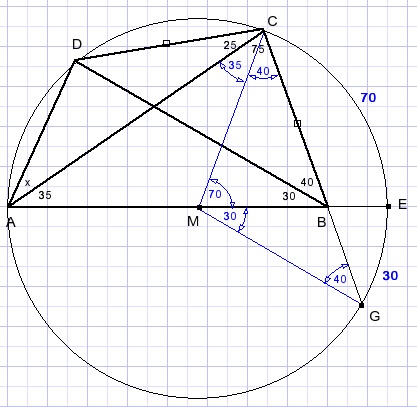
LCME = 70.
LACM = 70 - 35 = 35.... MA = MC.

LMCB = 75 - 35 = 40.
LMGC = 180 - 100 - 40 = 40.
MG = MC.

M is the center of the circle.
42.
Picture below shows circle arcs.
Prove that the red and blue shaded areas are equal.



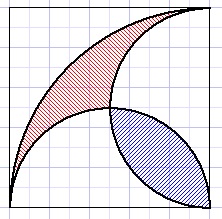
Solution




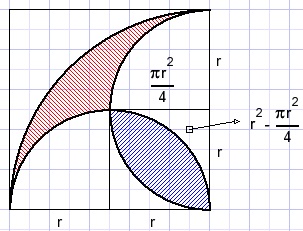
The red area:



The blue area:


43.
Show that:



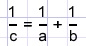
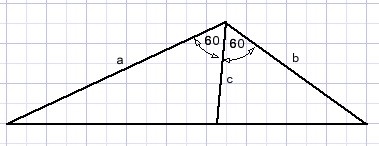
Solution 1

This solution is based on the bisectrix lemma:
    "the bisectrix of an angle divides opposing edge in parts having the same ratio as the sides of the angle."


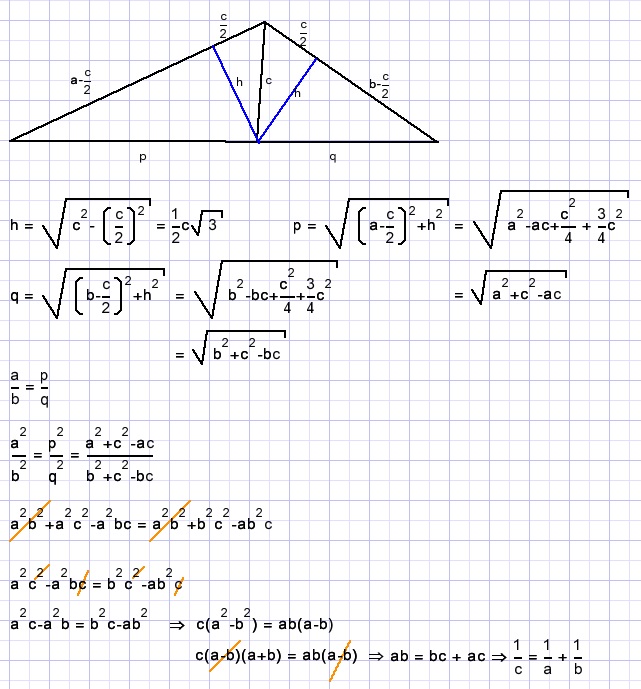
Solution 2

This solution is based on areas
    [ADC] + [DBC] = [ABC]
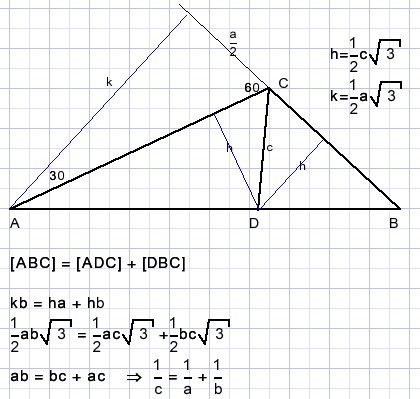
Note: [ABC] means the area of triangle ABC



Solution 3

This solution is based on trigonometry:
    "if two lines a and b make angle α the area of the triangle is 0,5absin(α)"


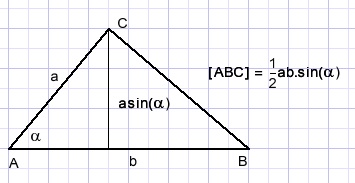
so: (see triangle at top of page)
0,5ab.sin(120) = 0,5bc.sin(60) + 0,5ac.sin(60)
because sin(120) = sin(60)
ab = bc + ac etc.

Solution 4

This solution is based on similar triangles.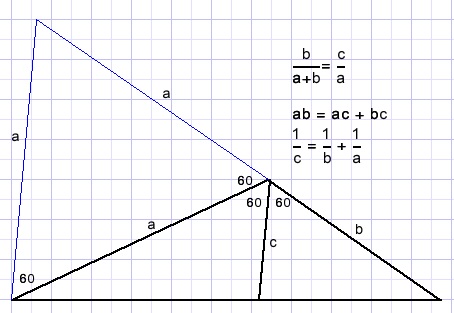


44.
Find the formula for the blue area.



All circles have radius r.

Solution







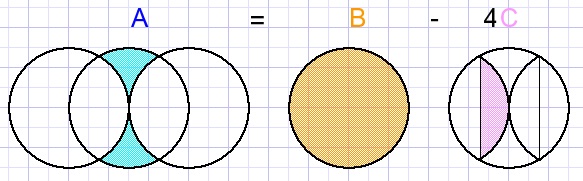
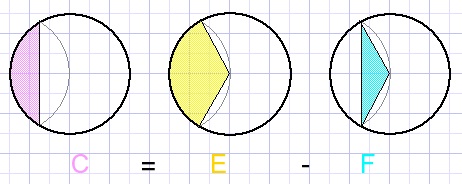
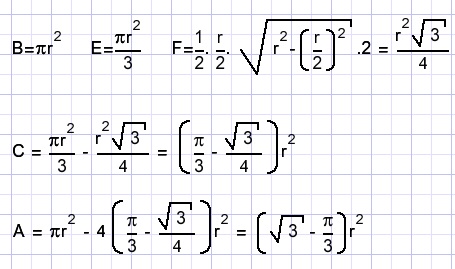
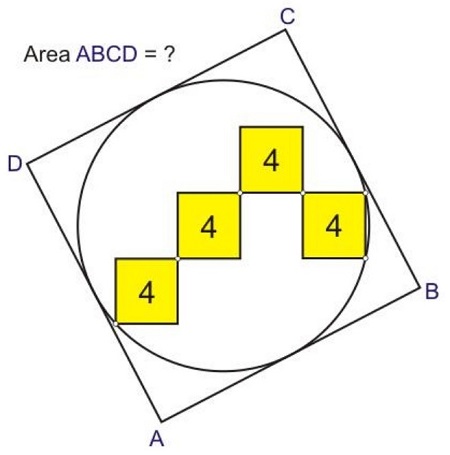
45.
Calculate the area of square ABCD.



Solution





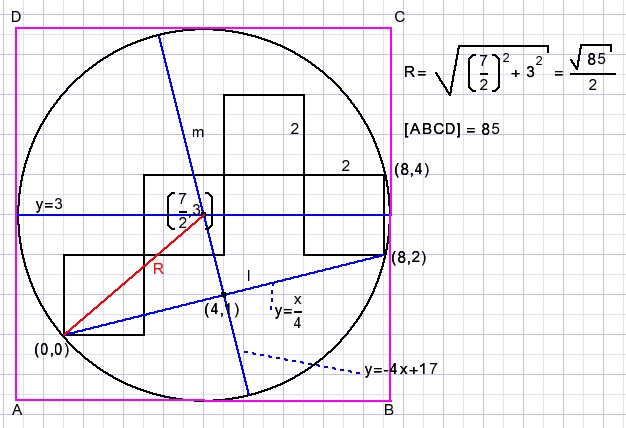
Explanation:

Origin of coordinate system: lower left of small square.
Line l has equation: y = 0,25x.
Center of line k is (4,1)
Line m has tangent -4....{product of perpendicular tangents is -1}
Center of line l is (4,1)
So:
1 = -4.4 + b
b = 17
Equation of m: y = -4x + 17.
Diameter of circle y = 3
3 = -4x + 17 ...... x = 7/2.

Pythagorean lemma to find radius of circle.
Area is the square of 2x radius.
46.
Given is square ABCD.
Calculate side x.



Solution 1.




    9sin(α) + 7cos(α) + 14sin(α) = x...............1)
    9cos(α) - 7sin(α) + 14cos(α) = x

    23sin(α) + 7cos(α) = 23cos(α) - 7sin(α)
    30sin(α) = 16cos(α)
    tan(α) = 16/30.....α=28,075
substitute in ....1) x = 17

Solution 2

Observe diagonal AC.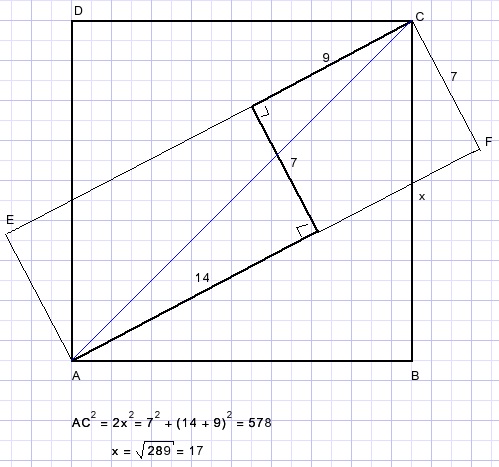


47.


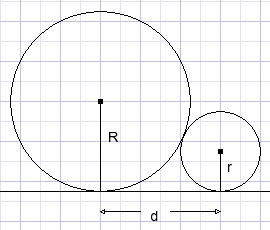
prove that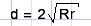

Solution



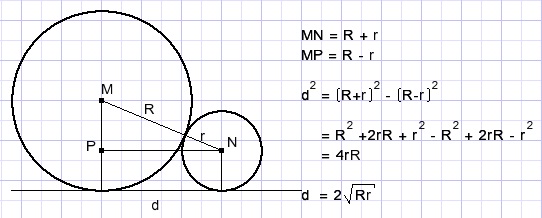
48.


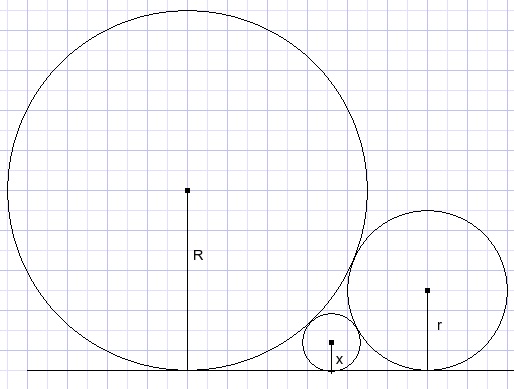
prove that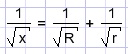

Solution


Use result of previous problem (47):


49.


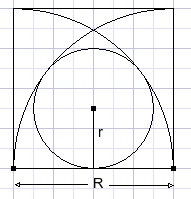
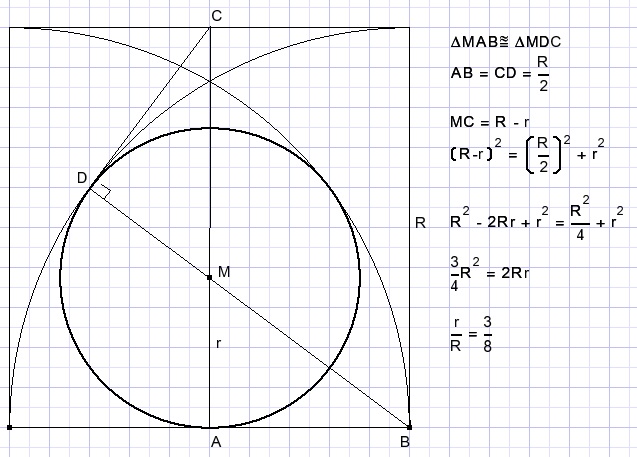
calculate the ratio

Solution