

| Geometry problem solutions4 (30..39) |
30.
Calculate angle x in picture below:
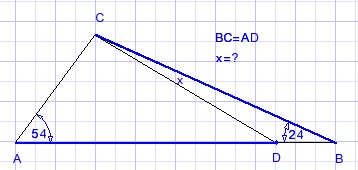
Solution
Shift BC parallel such that point B is on D.
(Picture enlarged for clearity)

E is shifted point C.
The angles colored red were calculated from the fact that
ΔADE is isosceles.
Shift ΔADE horizontaly until D reaches B and E is on C.
G is the shifted point A.

Add line BF with LCBF=24o.
AF is a straight line.
LAFB=78o, so BF = BC.
G,C,F are angles of a regular 15 polygon with center B.
First an intermezzo, see picture below:

MP rotates over angle 2α to MQ.
As a result SP rotates around S by angle α
Now the last step (picture reduced).
H is center of CF.
HK is diameter of the crcle.
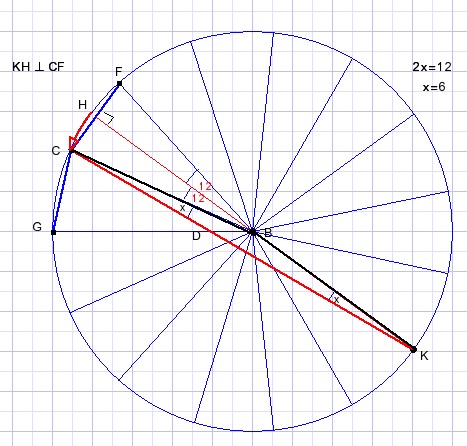
HB rotates over angle 12o to CB.
KH rotates 6o with center K to KC.
x = 6o
Postscript
My impression is that a more elegant solution must be possible.
Who helps?
31.
Calculate angle x in picture below.
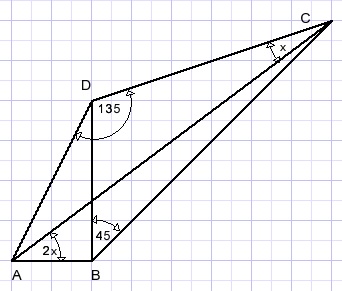
Solution
A quick guess seems x = 18 degrees, but this is just an approximation.A geometrical solution using compass and ruler seems impossible.
Below a trigonometrical solution using the sine rule.
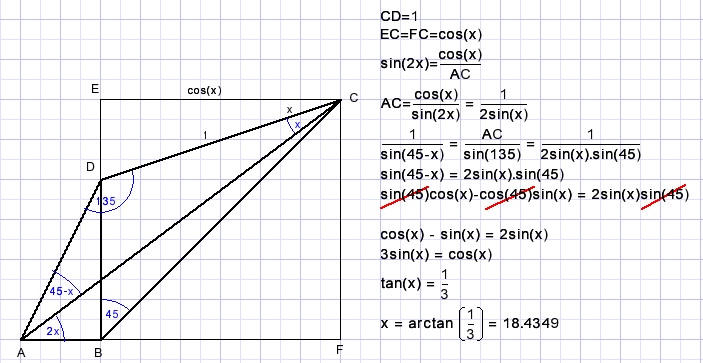
32.
In picture below is
-
AB=BC=CA=CD=AE.
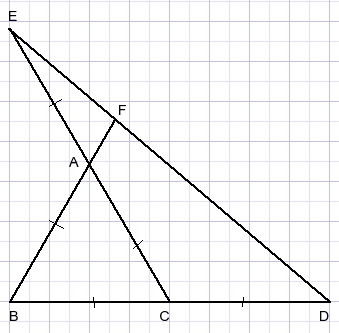
Solution
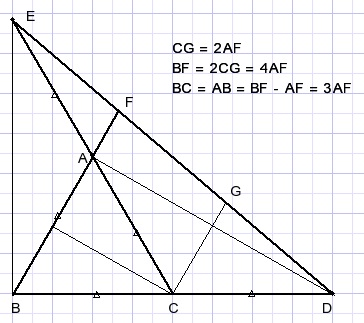
Draw CG || BFDraw line through C || AD.
Use similarity of triangles.
See :
33.
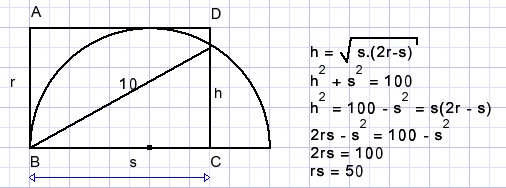
Given is a 180 degree circle arc and rectangle ABCD.
BD=10.
Calculate the area of the rectangle.
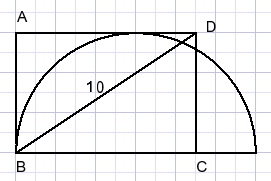
Solution
First this: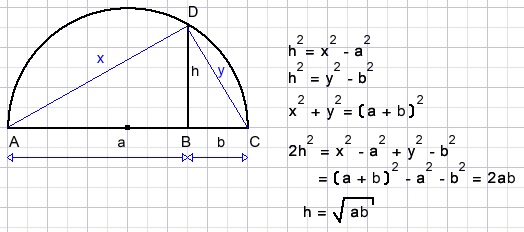
Let r be the radius of the arc.
Let BC=s.
See before:
34.
See picture below with given angles in square ABCD:
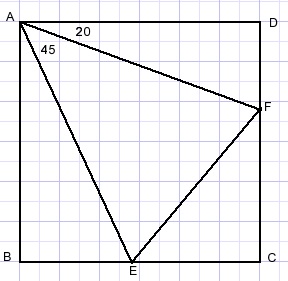
Question:
Calculate angle AEF.
Solution

Rotate ΔAFD around point A.
This results in ΔAGB.
Draw GF.
LBAE=25.
LGAE=20+25=45.
AE is bissectrix in isosceles triangle AGF.
So, GF is perpendicular to AE.
LFGB=70-45=25.
LGEA=LAEF=90-25=65.
35.
Calculate angle x in picture below.
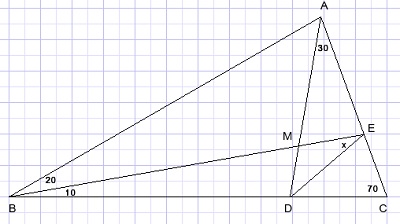
Solution (1)
This solution is my own.LBAC=50+30=80.
LBEA=10+70=80.
so:
BA=BE
Draw perpendicular bisector of AE.
Extend DE, F is the intersection with the perpendicaular bisector.
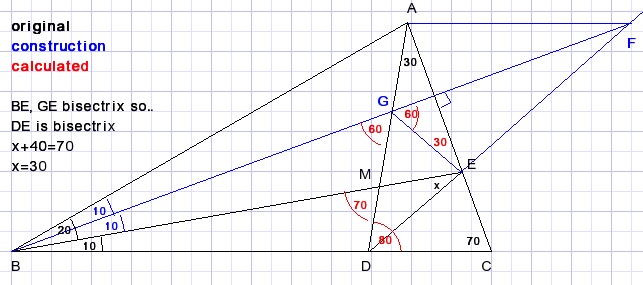
BF intersects AD in G.
Draw GE.
LFGE=60.
LBDG=60.
So:
LDGE=60.
GE is bisector of exterior angle of ΔBDG.
BE is bisector of LFBC.
Bisectors of a triangle intersect at one point.
So DE also is bisector of LADC=80.
x = 70-40 = 30 degrees.
Solution (2)
This solution is of Nelson Tunala and was found in Facebook group "classical mathematics".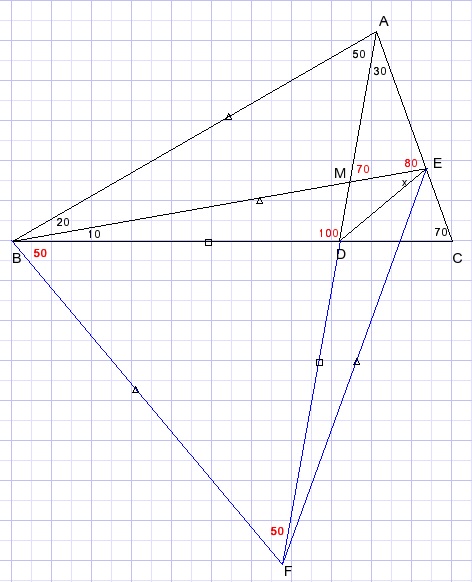
BA=BE (see solution 1)
Extend AD, point F is such that BF=BA.
LBAF=LBFA=50
BE=BF, LEBF=60 so ΔBEF is regular.
LDBF=LDFB=50 so BD=DF.
so:
ΔBED is congruent with ΔFED
LBED=LFED.
x = 60 / 2 = 30 degrees.
Note
The picture has several similar triangles.I tried to prove that DA : DC = EA: EC
which is the case when DE is a bisector.
36.
Prove that r2 = ab.
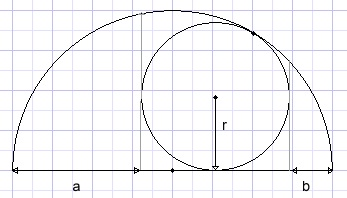
Solution
First this: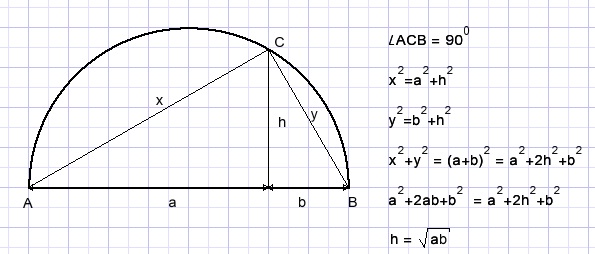
There we go:
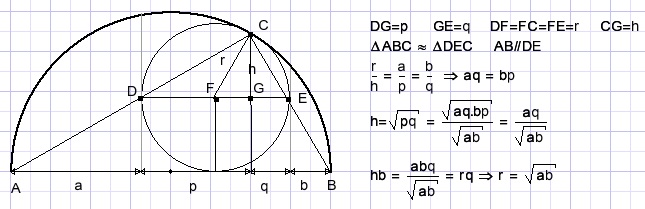
37.
Calculate distance x in rectangle below:
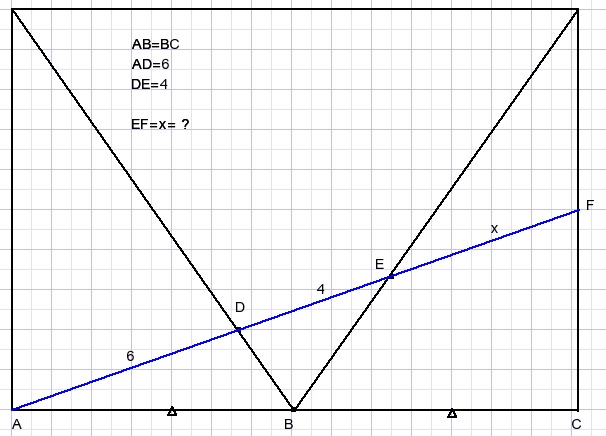
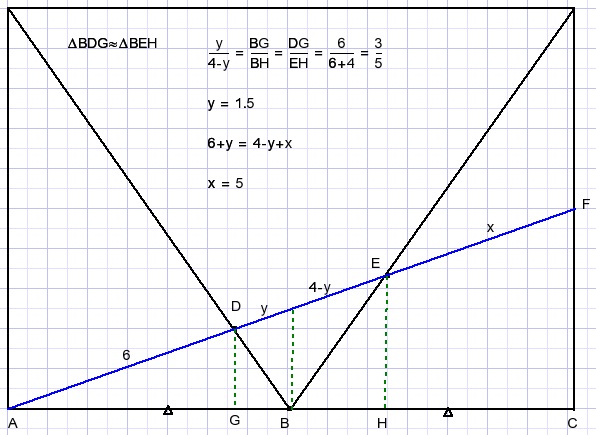
Solution
38.

ABCD is a rectangle, AB=4 and AD=3.
Point E is positioned randomly at line CD.
Calculate the area of triangle EFG.
This problem is interesting for two reasons:
1. the area of triangle EFG is independent of the position of E.
2. I describe two solutions, one with some algebra, a second without.
Notation: the area of triangle ABC is written as [ABC]
Solution (1)
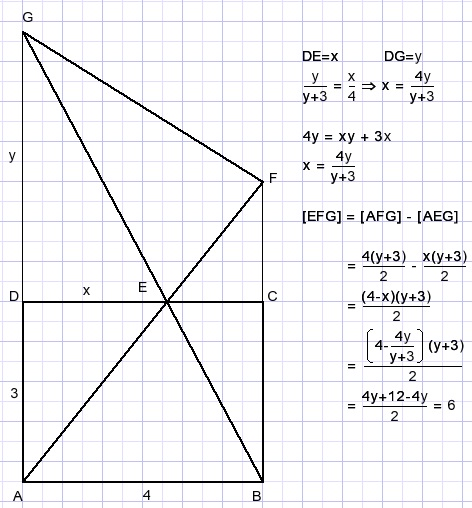
Solution (2)
[AFG] = [ABG]..........result of equal base and height.
[ABE] = [ABG] - [AEG]
[EFG] = [AFG] - [AEG]
[EFG] = [ABE] = 3*4/2 = 6
39.
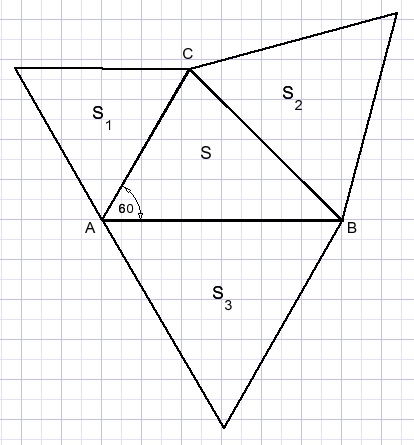
See picture below.
The triangles other than ΔABC are equilateral.
LA = 60 degrees.
Prove that area S + S2 = S1 + S3.
Preface.
The area of a triangle equals base * height/2.
An equilateral triangle with sides z has area:
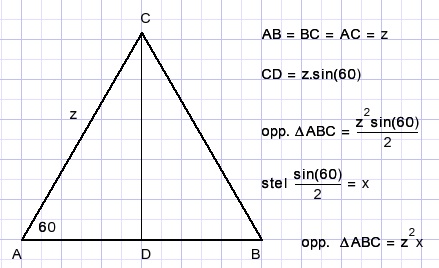
See above piture , let :
- AB=c
- AC=b
- BC=a
Apply cosine rule in ΔABC:
-
a2 = b2 + c2 - 2bc.cos(60)
cos(60) = 0,5....
a2 = b2 + c2 - bc
vermenigvuldig met x:
a2x = b2x + c2x - bcx
a2x = S2
b2x = S1
c2x = S3
bcx = S....
S2 = S1 + S3 - S
S + S2 = S1 + S3

