some calculations in plane geometry 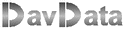This article describes some formula's in plane geometry. They are nice applications of algebra. 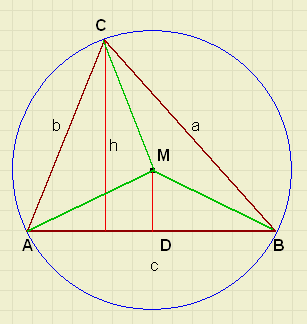List of contents: the area of a triangle the projection formula Stewart's formula the length of the median the bisector formula the radius of the circumscribing circle the radius of the inscribed circle the radius of the escribed circle kissing circles intersecting circles the area of a triangle In cases where the length of the sides of a triangle are known, but not the height, a formula for the area of the triangle without this height would be of help. Please look at the picture right: the base, opposite angle A, has length a. BD = x, so DC = a - x. AD = h. Side b is opposite angle B, side c is opposite angle C. There we go: application of the theorem of Pythagoras in triangles ABD and ADC results in two equations: ­ ­ c 2 = h 2 + x 2 b 2 = h 2 + (a − x) 2 ­ or: ­ ­ h 2 = c 2 − x 2 h 2 = b 2 − (a − x) 2 ­ so c 2 − x 2 = b 2 − (a − x) 2 and c 2 − x 2 = b 2 − (a 2 − 2 a x + x 2) c 2 − x 2 = b 2 − a 2 + 2 a x − x 2 c 2 = b 2 − a 2 + 2 a x 2 a x = a 2 − b 2 + c 2 x =  a 2 − b 2 + c 2 2 a this value of x, substituted in h2 = c2 - x2 = (c - x)(c + x): h 2 =  æ c −  a 2 − b 2 + c 2 2 a ö ­ ­ è ø   æ c +  a 2 − b 2 + c 2 2 a ö ­ ­ è ø h 2 =  2 a c − a 2 + b 2 − c 2 2 a  ·  2 a c + a 2 − b 2 + c 2 2 a h 2 =  −(a 2 − 2 a c + c 2 − b 2) 2 a  ·  a 2 + 2 a c + c 2 − b 2 2 a h 2 =  −((a − c) 2 − b 2) 2 a  ·  (a + c) 2 − b 2 2 a h 2 =  b 2 − (a − c) 2 2 a  ·  (a + c) 2 − b 2 2 a h 2 =  (b − a + c) (b + a − c) 2 a  ·  (a + c − b) (a + c + b) 2 a h 2 =  (−a + b + c) (a + b − c) (a − b + c) (a + b + c) 4 a 2 This formula can be simplified with a tric. If s is half of the circumference, than ( a + b + c) = 2s (-a + b + c) = 2s - 2a ( a + b - c) = 2s - 2c ( a - b + c) = 2s - 2b and the formula changes to h 2 =  2 s (2 s − 2 a) (2 s − 2 b) (2 s − 2 c) 4 a 2 h 2 =  4 a 2  s (s − a) (s − b) (s − c) h =  2 a   \ s (s − a) (s − b) (s − c) and because tghe area A =  a h 2 A =  \ s (s − a) (s − b) (s − c) with this formula, the area A of a triangle can be calculated if the sides a,b,c are known (but not the height). An Example A triangle has sides of length 7, 8 and 11. So, s = (7 + 8 + 11) / 2 = 13. 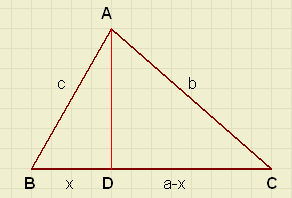The area O =  \ 13 (13 − 7) (13 − 8) (13 − 11)  = 27 , 928 m 2 the projection formula Application of the Pythagoras theorem: a2 = h2 + (c - p)2 a2 = b2 - p2 + c2 - 2cp + p2 a2 = b2 + c2 - 2cp the projection formula: a2 = b2 + c2 - 2cp remark: If point D is right of B, -2cp changes into +2cp. The reader may verify this. p is the projection of b to c. hence the name. Stewart's formula P is a random point on base AB. P divides AB in lines c1 and c2. The formula of Stewart calculates the length of CP, if the sides a,b,c of the triangle and the position of P are kwown. Application of the projection formula in triangles APC and ABC : ­ ­ C P 2 = b 2 + c1 2 − 2 c1 p a 2 = b 2 + c 2 − 2 c p ­ multiplication of the first line with (c) and the second with(c1): ­ ­ c C P 2 = b 2 c + c c1 2 − 2 c c1 p c1 a 2 = b 2 c1 + c1 c 2 − 2 c c1 p ­ Subtract the lower equation from the upper: c C P 2 − c1 a 2 = b 2 c − b 2 c1 + c c1 2 − c1 c 2 c C P 2 = c1 a 2 + b 2 c − b 2 c1 + c c1 2 − c1 c 2 c C P 2 = c1 a 2 + b 2 (c1 + c2) − b 2 c1 + c c1 2 − c1 c 2 c C P 2 = c1 a 2 + c2 b 2 + c c1 (c1 − c) c C P 2 = c1 a 2 + c2 b 2 + c c1 (c1 − c1 − c2) c C P 2 = c1 a 2 + c2 b 2 − c c1 c2 this is Stewart's formula: c.CP2 = c1a2 + c2b2 - 2c.c1.c2 the length of the median If AP = PB then CP is the median of angle C. 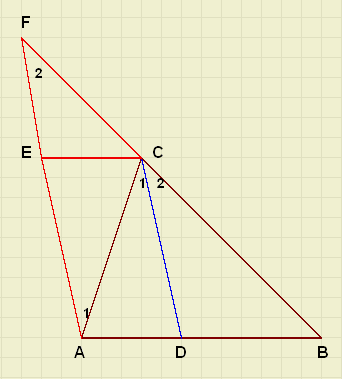For c1 = c2 and CP = Zc Stewart's formula changes into: c Zc 2 =  c 2  a 2 +  c 2  b 2 − c ·  c 2  ·  c 2 Zc 2 =  a 2 2  +  b 2 2  −  c 2 4 this is the formula for the median of a triangle: Zc 2 =  a 2 2  +  b 2 2  −  c 2 4 the bisector formula CD divides angle C in equal parts. First a theorem of plane geometry to get a relation between a,b and c1,c2. Given: DABC CD divides LC. we prove that: In a triangle, the bisector divides the opposite side in parts with the same ratio as the sides of the angle: AD : DB = AC : BC Proof: make BC longer draw AF || CD and EC || AB because of parallellism of lines: LC1 = LA1 LC2 = LF so LF = LA1 in a triangle, sides opposite equal angles are also equal, so AC = FC because of similarity of DECF and DDBC EC : DB = FC : BC because ADCE is a rhombus: EC = AD so: AD : DB = FC : BC and because FC = AC AD : DB = AC : BC back to the bisector formula. Starting with a b  =  c2 c1 we write: ac1 = bc2 Stewart's formula c C P 2 = c1 a 2 + c2 b 2 − c c1 c2 is changed into c C P 2 = a b c2 + a b c1 − c c1 c2 and c C P 2 = a b (c1 + c2) − c c1 c2 C P 2 = a b − c1 c2 The bisector formula is C P 2 = a b − c1 c2 If c1 and c2 are unknown than from: ­ ­ a c1 = b c2 c1 = c − c2 ­ we may calculate c1 =  b c a + b c2 =  a c a + b c1 en c2 substitution into the bisector formula results in C P 2 =  4 a b (a + b) 2  s (s − c) s is half of the circumference of the triangle. Calculations are left to the reader. 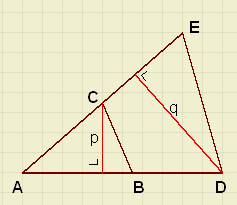the radius of a circumscribing circle First another theorem: If two triangles have a common angle, then the ratio of their areas is equal to the ratio of the products of their sides forming the angle. DABC and DADE have LA in common. area.DABC : area.DADC = (p.AB) : (p.AD) = AB : AD area.DADC : area.DADE = (q.AC) : (q.AE) = AC : AE multiplication by AC and AD: AB : AD = (AB.AC) : (AD.AC) AC : AE = (AD.AC) : (AD.AE) so area.DABC : area.DADE = (AB.AC) : (AD.AE) In the picture right, M is the middle of the circumscribing circle of DABC. applying the theorem of Thales: LDMB = 0.5*LAMB = LC so: area DABC : area DDMB = (AC.BC) : (DM.BM) but also: area DABC : area DDMB = ( c 2  h ) : ( c 4  D M ) because BM = R {the radius} AC = b BC = a AB = c follows:   a b D M.R      =    c 2  h c 4  D M and R =  a b 2 h we know that area DABC = 0.5hc, so h = 2*area DABC / c and the length of radius R of the circle is: R =  a b c 4 A where A is the area of the triangle ABC. the radius of inscribed circle 2 * area DABC = ar + br + cr = r(a + b + c) so: r =  A s Remark: s is half the circumference of the triangle. 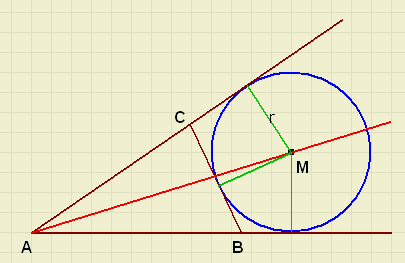the radius of the escribed circle The radius ra is ra =  A s − a where: BC = a AC = b AB = c (a + b + c) / 2 = s The proof is left to the reader. Suggested exercises: r, ra , rb , rc are the radius of the in- and escribes circles of DABC. A is the area of DABC. prove that: 1. A =  \ r ra rb rc 2. 1 r  =  1 ra  +  1 rb  +  1 rc kissing circles Two circles with radius r and R are placed on a line. We derive a formula for the distance d = AB. Application of the theorem of Pythagoras: (R + r)2 = d2 + (R - r)2 R2 + 2Rr + r2 = d2 + R2 - 2Rr + r2 d = 2  \ R r Suggested exercise: In the picture above, a small circle with radius x just fits between the line and the circles with radius r and R. 3. using the derived formula for d, prove that 1 \ x  =  1 \ R  +  1 \ r 4. see picture right. 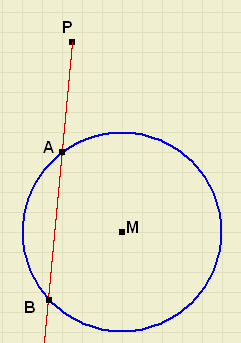P is a fixed point. A and B are randomly choosen points on the circle. Prove, that PA.PB is a constant value. (called: the power of P relative to the circle) intersecting circles Circles with radius R and r and d = MN < R + r intersect. See picture right. We derive a formula for the length of MP. The picture shows MT = d - r NU = d - R We add a point Q on line MN such, that MQ = QN. Now R2 - MP2 = r2 - NP2 or MP2 - NP2 = R2 - r2 (MP + NP)(MP - NP) = (d)(MQ + QP - (QN - QP)) = 2d.QP because 2d.QP = R2 - r2 Q P =  R 2 − r 2 2 d M P = M Q + Q P =  d 2  + Q P M P =  d 2 + (R 2 − r 2) 2 d Suggested exercise: see picture above. 5. find also formula's for NP, TP, UP.