Formula Translation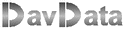

The Project

This article describes the translation of several types of mathematical equations into a sequence
of basic arithmetic operations.
Such a process is also known as "parsing" and is necessary when plotting functions or using them in spreadsheets.
Years ago, I designed the algorithm for my equations grapher Graphics-Explorer.
However, at a second glance, this Delphi source code is rather hard to read.
So I have rewritten the code into a more comprehensible form.

The Delphi-7 project consists of 3 units:
    - unit1: form with buttons, TEdit for entering formulas and a paintbox to show graphics and tables
    - xlate: holds the code for the translation and the calculations
    - eqdrawer: holds procedures to draw the different type of equations using the xlate unit
Form1 and unit1 make a simple excerciser to test the translation.
xlate also holds debug code that may be switched on and off.
This code allows for the display of the tables generated in the translation process.

Click [ here ] to load the excersiser program.
Click [ here ] to load the complete Delphi-7 project.
Click [ here ] for the complete source listing of the translate unit.

Below is a snapshot of the exerciser, showing the function y = x*sin(3x)

Donations

Designing software is time consuming.
I offer this software for free.
However, if you make commercial use of it, or appreciate it otherwise,
be so kind to make a donation to support my website.

Formulas, Equations and Functions

A formula is a calculation which contains unknown numbers.
These numbers are represented by a character.
An example is the formula for the volume V of a sphere having radius R :....... V = (4/3)pR3
Here, p is a constant (3,14.......) and R is a variable.
By substituting p with enough digits for the needed accuracy and R
with the length of the radius, we obtain V for this sphere after the necessary calculations.

In the above example, R is the independent variable (we may give it any positive value) and
V is the dependent variable.
When the context is unknown, it is customary to call 'x' the independent and 'y' the dependent variable.

The form .....y = ....some formula with x...... is called a function
For each value of x we may calculate y.
Each pair (x,y) may represent a dot in a coordinate system.
All dots together make the graph of the function.

The form ....x = ....some formula with y........is called an inverse function.
A substituted value of y yields a value of x.
Notice that an inverse function is the result of mirroring a normal function in the line y = x.

The functions above cannot represent graphs as a circle, where a single value of x may have 2 values of y.
In that case a so called parametric function may be used.
The tric is to have an intermediate variable (in our case V) and make both x and y a function of V.
Using my translator you may simply write:
    y = 5sin(v) ; x = 5cos(v) ........for a circle with it's center at (0,0) and radius 5
In rare cases as graphs of trifoliums and the like, functions do not exist.
These graphs are the result of equations like
    .....x.....y.... = ....x....y......
Left and right of the equal sign is a formula with x and y.
The graph is the set of all dots (x,y) where the '= ' is true: the same value left and right of the equal sign.
My translator and drawing procedures also support this so called 'implicit' functions, however the processing time
is longer.
So, writing y = 2x - 5 yiels the same graphic as y - 2x = 5 but the latter is slower.

All functions (normal, inverse, parametric, implicit) use the same translator and result in the same tables.
The drawing procedures however are different.

To summarize the supported functions / equations:
    typenameexamplemeaning
    1normaly = 3x2 -2x + 1parabolic function
    2inversex = 3sin(y)inverse sine function
    3parametricy = 3sin(x) ; x = 3cos(x)circle
    4implicitx2 + y2 = 9same circle as in type 3

Operators and priorities

A calculation like 1 + 3*2 + 5*32 cannot be made from left to right as operations have different priorities.
Also calculations between (.......) have priority as in 3*(10 -6) where 10 - 6 has to be calculated first.
The following table shows the priorities of the operations supported
    namesymbolpriorityexample
    function...7log(x)
    exponentiation^6x^3
    unairy --5-sin(x)
    multiplication*43*x
    division/4x/5
    addition+3x+5
    subtraction-3x/5
    transfer=2y = 17
    separator;1y = 1; x = 2
Note: the ; operator is a dummy with the lowest priority.
It keeps the x and y variables separated in parametric functions.

An intrinsic (type 4) function like........x^2 + y^2 = 15x + 22y is changed into .....v = x^2 + y^2 - 15x + 22y
before the translation process.
The - operator is assigned a priority of 2, the = operator a priority of 1.
So, if a set of (x,y) satisfies the equation then v = 0.

Determining the type of equation

The translator is called by
    procedure xlateEquation(s : text; var xcode: byte);
The formula text is s.
The returned xcode byte will be zero for a successfull translation and unequal to zero for a particular error.
Before the translation starts the text is converted to lower case characters and copied in string "basetext".
Also a blank character is appended to the string to mark the end. This facilitates the translation.
xlateEquation(..,..) then calls procedure detecttype to find out which type was presented.

Detecttype counts the number of x , y, = and ; characters, recording also their position in the string
while ignoring blanks.
This is accomplished by an array with separate columns for the x, y, = and ; characters and plenty of rows.
If an x is found at position 1 of the string, the number 1 is written in the next free position of the x column.
If a ; is found at position 15 in the string, then 15 is written in the column for the ;
The height of the column is the amount of characters x, y, = , ; encountered in basetext.

Detection of a type 1 function:
    - only one y found at position 1 {remember, blanks are ignored}.... and
    - only one = found at position 2 ....and
    - no ; detected
Detection of a type 2 function:
    - only one x found at position 1.......and
    - only one = found at position 2........and
    - no ; detected
Detection of a type 3 function:
    - one ; detected....and
    - two = characters detected.......and
    - only one x found in position 1....and ... only one y found after ;.....or
    - only one y found in position 1....and ... only one x found after ;
Detection of a type 4 equation:
    - no type 1,2,3 detected before ..........and
    - no ; found.........and
    - only one = found
Please refer to the source code for details.
Array cp[x...; , rows] holds the positions of the characters x,y,=, ;
Array cc[x..;] holds the number of characters in each column of cp[ ]

Data Structures

The numbers for all calculations are stored in an array REG[1..67] of double.
Following table shows the assignments:
    register numberpurpose
    1..29intermediate results during calculations
    30..59constants found in basetext string
    60x
    61y
    62v
    63a
    64b
    65c
    66pi
    67e
a,b,c are constants. Their value may be changed without the necessity to retranslate the formula.
pi = 3.14.... and e is the base of the natural logarithm.

operators and function are assigned an operation code:
    codeoperationname
    1+addition
    2-subtraction
    3*multiplication
    4/division
    5^exponentiation
    6-unairy -
    7=transfer
    8;separator
    9not used.
    10sinsine
    11coscosine
    12tantangent
    13asininverse sine
    14acosinverse cosine
    15ataninverse tangent
    16sqrtsquare root
    17loglogarithm base 10
    18lnlogarithm base e
    19exppower of e
    20absabsolute
    21introunded to integer

The Postfix Table

This is an interim table in the translation process.
Procedure makePFT builds the table.
It's entries are of type TPostfix: 
type TPostfix = record
                 reg      : byte;
                 opcode   : byte;
                 priority : byte;
                end;
				
const maxPFT     = 60;	

var PFT       : array[1..maxPFT] of TPostFix;
    pfti      : byte; //#entries in PFT
Building the postfix table is the next step after the equation type was determined.
Besides of building the table, the makePFT procedure:
    - places constants in registers 20...59 in the sequence of their occurrence
    - inserts * operators between
      - )(
      - constants or variables and (.....example: 3( --> 3*(........or .....x( --> x*(
      - constants or variables and ).....example: )3 --> )*3........or......)x --> )*x
      - constants and functions ......example: 3sin(x) --> 3*sin(x)
      - variables and constants.......example: 3x --> 3*x .. or x3 --> x*3
    - performs the syntax checking
In TPostfix,
    reg.........is the register number
    opcode...is the operation code, see table above
    priority....is the priority of the operation
The priority is the sum of the biaspriority (variable biasprio) and the priority of the operation.
The biaspriority is increased by 10 after an ( opening parenthesis and decreases by 10 after a ) closing parenthesis.
So, x + 3 has priority 4, but (x + 3) has priority 14.

Examining the character string of an equation we notice the structure
    | variable or constant | operator | variable or constant | operator | ......................
In the postfix notation the string is written as
    | variable or constant | operator |
    | variable or constant | operator |
    | variable or constant | operator |
    ............................
Then a third column is added to the table to indicate the priority of the operation.
The objective is later to select the table entry with the highest priority to build a final table
holding all operations in descending priority.

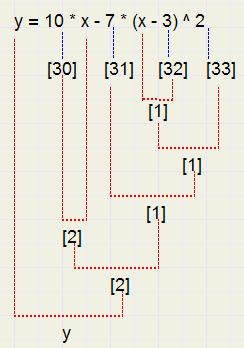
Here is an example what the Postfix table (PFT) looks like after translating
y = 10x - 7(x-3)^2:
    regopcodepriority
    y=2
    [30]*4
    x-3
    [31]*4
    x-13
    [32]^6
    [33]...0
Note: constants are stored in registers 30,31,....as they occur in the string, so
[30] = 10, [31] = 7, [32] = 3, [33] = 2

Let's take a closer look at the way the table is built.
The characters of basetext are looked at by groups:
    'a' ...'z'
    '0'..'9', decimal point
    (
    )
    =
    -
    + * / ^
    space
    ;
The equation string basetext is scanned character by character.
A case statement handles execution of a character according to it's group above.
Action depends however on the current process or previous findings.
The latter is indicated by variable scan where 
type Tscan = (scNone,scAlphaScan,scNumScan,scConstant,scVariable,scFunction,
              scOperator,scOpen,scClose);
    scNone:nothing happened....{at start, after = or ; }
    scAlphascan:scanning the name of a variable or function
    scNumscan:scanning a number
    scConstant:numeric constant found
    scVariable:variable found
    scFunction:function found
    scOperator:operator found
    scOpen:( found
    scClose:) found
So, a character read from the basetext string is presented to a case statement to test for it's group.
Then for each group a new case statement tests for the state of the scan variable.
From this point in the code, helper procedures are called to build the Postfix table.
These are the helper routines that do the construction work:
    procAlpha:test alpha string for being variable or function. Get register number or operator code.
    procNum:test numeric string for being a constant, enter constant in register
    procUminus:handle unairy - as in ...( -x + 4)
    procOpen:increase biaspriority by 10
    procClose:decrease biaspriority by 10
    multInsert:insert a * operator for multiplication, as between ) (
The nested case statements take care of the syntax checking.

Example:
procAlpha will be called if scan = scAlphascan ...{we are reading characters from basetext
that might become a variable or function} and we encounter:
a blank, ( , ) , numeric character, ; or an operator.
We look at the first code lines of the case statement: 
 for i := 1 to length(basetext) do
  begin
   c := basetext[i];
   case c of
    '(' : begin
           case scan of
            scNumScan : procNum;
            scAlphaScan : procAlpha;
           end;
           case scan of
            scClose,
            scVariable,
            scConstant : multinsert;
           end;//case
           procOpen;
          end;// '('

    ')' : begin
           case scan of
            scOpen,
            scOperator,
            scfunction : errorcode := 7;
            scNumScan  : procNum;
            scAlphaScan: procAlpha;
           end;//case
          procclose;
          end;//')'
		  ......................
Note: errorcode 7 is the code for syntax error.
In this case we may have found ......sqrt) , which is illegal.

Note: after the procAlpha procedure the scan variable is either scVariable or scFunction, whatever was detected.
After the procNum procedure, scan = scConstant.
after multInsert , scan = scoperator

Refer to the source code of the xlate unit for the details such as actions of the helper procedures
inside procedure makePFT.

Building the Director table.

This is the final table of the translation process.
Procedure makeDRT builds the table.
The xlateEquation procedure calls makeDRT if the Postfix table is built sucessfully, which is the case
if the errorcode = 0. 
type TDirector = record
                  opcode : byte;
                  dest : byte;
                  src1 : byte;
                  src2 : byte;
                 end;
				
const maxDRT = 60;	

var DRT    : array[1..maxDRT] of Tdirector;
    dix    : byte;//index for DRT during calculations
    valid  : boolean;//during calculations
    DRTtop : byte; //#entries in DRT
The director table (DRT) holds all operations sorted to priority from high to low.
dest is the destination register, src1 and src2 are the source registers.
For the Postfix table above { y = 10x - 7(x-3)^2 } , the DRT is:
    opcodedestsrc1src2
    -[1]x[32]
    ^[1][1][33]
    *[2][30]x
    *[1][31][1]
    -[2][2][1]
    =y...[2]
The next figure shows the calculations and intermediate results on a downward the time scale.
[1] means : scratch register number 1.
Procedure makeDRT searches the PFT for the operation having the highest priority.
If necessary, a scratch register is assigned to hold intermediate results.
The operation and registers are filled in in the DRT and the operation is removed from the PFT.
makeDRT has 3 helper procedures:
    function getfreeReg : bytereserve and return a free scratch register for intermediate results
    procedure freeReg(k : byte)free Register k for future assignment
    procedure ShiftUpPFT(n : byte)shift [n+1] --> [n], [n+2] --> [n+1] ......
variable regreserve has bit i set for a free register i.
Initially, regreserve is preset to $3ffffffe for free scratch registers 1..29.

Say, line j of the PFT holds the operation with the highest priority.
Then source operand 1 (src1) of the DRT entry is set to reg of line j of the PFT.
Source operand 2 (src2) is set to reg of line j+1 in the PFT.
The opcode in DRT is set to the opcode of line j in the PFT.
What about the dest (destination) register in the DRT?
    - if only one of the source operands is a scratch register, then dest is that scratch register.
    - if both src1 and src2 are scratch registers then src1 becomes the destination register
    - if both registers are variables or numeric constants, then a scratch register is assigned for dest
    - if x,y or v is the reg of line j in the PFT, than dest is the same x,y or v
The situation is coded into variable regcode and then a case statement examining regcode
takes the appropriate action.
Note: in case of a function or unairy - , the reg field in the PFT equals 0.
The operand is found as field reg on the next PFT entry.
Functions and the unairy - only use src2, src1 = 0.
After shifting up the PFT to eliminate the operation just added to the DRT, the PFT reg field is set to the destination register.

Let's break down the above equation step by step, breaking down the PFT while building the DRT.
{y = 10x - 7(x-3)^2 }
    Postfix table PFTdirector table DRT
    regopcodepriority
    y=2
    [30]*4
    x-3
    [31]*4
    x-13
    [32]^6
    [33]...0
    opcodedestsrc1src2
    -[1]x[32]
Scratch register 1 is assigned for the result.
    Postfix table PFTdirector table DRT
    regopcodepriority
    y=2
    [30]*4
    x-3
    [31]*4
    [1]^6
    [33]...0
    opcodedestsrc1src2
    -[1]x[32]
    ^[1][1][33]
register 1 holds the result
    Postfix table PFTdirector table DRT
    regopcodepriority
    y=2
    [30]*4
    x-3
    [31]*4
    [1]..0
    opcodedestsrc1src2
    -[1]x[32]
    ^[1][1][33]
    *[2][30]x
register 2 holds another intermediate result
    Postfix table PFTdirector table DRT
    regopcodepriority
    y=2
    [2]-3
    [31]*4
    [1]..0
    opcodedestsrc1src2
    -[1]x[32]
    ^[1][1][33]
    *[2][30]x
    *[1][31][1]
    Postfix table PFTdirector table DRT
    regopcodepriority
    y=2
    [2]-3
    [1]..0
    opcodedestsrc1src2
    -[1]x[32]
    ^[1][1][33]
    *[2][30]x
    *[1][31][1]
    -[2][2][1]
    Postfix table PFTdirector table DRT
    regopcodepriority
    y=2
    [2]..0
    opcodedestsrc1src2
    -[1]x[32]
    ^[1][1][33]
    *[2][30]x
    *[1][31][1]
    -[2][2][1]
    =y...[2]
And the translation is completed.

Please use the exerciser in debug mode to see the PFT and DRT of other equations and functions.

Syntax

Syntax checking is done during the construction of the PFT.
The main rule is that operators and constants, variables or functions must alternate.
Two successive operators such as - - 5 are illegal. Instead, write - (-5) which is OK.
Also legal is : y = - x or y = - cos(5x), where the - is a unairy operator.
Keep in mind the difference between - 2^4 { = - 16} and (-2)^4 { = 16}
After a function , a ( must follow. Example: sin(3x).
The * multiplication operator is inserted between )..( , numeric constants and variables or functions
and between ( or ) and functions, numeric constants or variables.
Examples:
    y = 3sin(x) .........y = 3*sin(x)
    y = (x-1)sin(x).........y = (x-1)*sin(x)
    y = sin(3x)............y = sin(3*x)
    y = (x-1)(x-2)............y =(x-1)*(x-2)
    y = a(x-1).............y = a*(x-1)
Parenthesis may be nested 20 levels deep.
A ( must be matched by a ) at each side of = or ; operators.

The following is illegal:
    y = xsin(x)............'xsinx' is an unrecognized string. Use x*sin(x)
    y = ab..............'ab' is an unrecognized string, use a*b
A translation produces an error code. Zero indicates a successfull translation.
If the errocode is nonzero, function getmessage(errorcode) gives a string with the decription of the error.

Calculations

Now with a completed director table it is easy to make calculations.
Just perform all basic operations in the table from top to bottom.
After the translation, the values of a, b, c still may be changed. Retranslation is not needed.
For a type1 function, before calculation we have to set the value of x by calling setX(...).
Then procedure calculate(var OK : boolean) is called to do the job.
The OK flag will be true after an error free calculation and false after an error
such as
    - division by zero
    - logarithm of a negative number
    - overflow
    - square root of a negative number
After the calculation the getY function returns y.

For each operator or function there is a small procedure that makes the calculation.
A try....except....structure takes care of any arithmetic errors.
Variable dix is the index into the DRT and it runs from 1 to DRTtop.

For a type2 function we have to set y using the setY(..) procedure and getX returns the calculated x.

For a type3 function, use setV(..) and later the getX and getY functions to get x and y.

For a type4 function both x and y have to be set and the result is returned by calling getV.
Remember that a type4 equation, such as x2 + y2 = 25, is modified to
v = x2 + y2 - 25, where the - operation has priority 2 and the = has priority 1.
So, v will be zero if the equation is true for a (x,y) pair.

The exerciser

The exerciser is programmed in form1 and unit1.
It provides a TEdit to enter equations and buttons to start translation or set a,b,c constants.
Also there is a checkbox to switch on debugmode, a label to display results and a 640 * 480 pixels paintbox
for the display of the registers for numeric constants, the postfix- and the director tables.
The exerciser has been kept very simple intentionally.
The coordinate system in paintbox1 has (0,0) at pixelposition (320,240),
x runs from - 8....+8 and y from -6....+6. The scale is 40 pixels per cm.

Please look at fxlate2.html for a description of the paint procedure for each equation type.