floating point numbers

Exploring Floating Point Formats

download the test program

download the complete Delphi-7 project

see the program source code

Introduction

In this article we explore two IEEE floating point formats implemented by Intel.
At the top of this page, click the lightning icon to load a test program.
This program accepts floating point numbers and shows the internal bit representation.

below is a picture of the program:

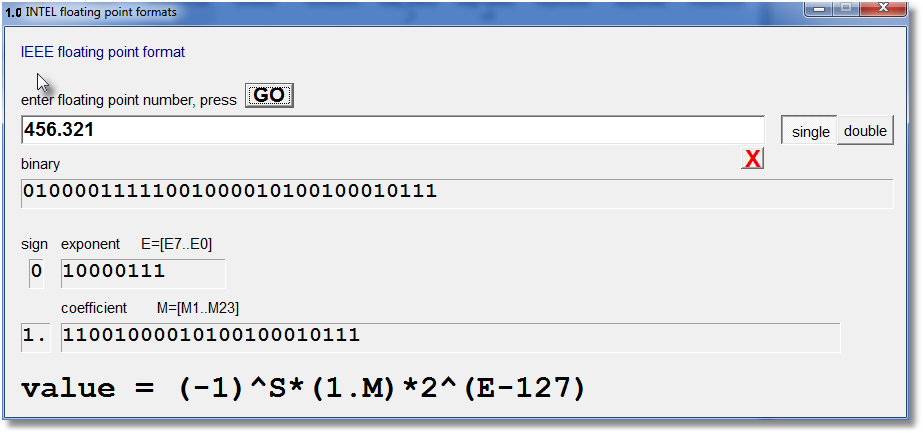
Floating point: the scientific notation

Floating point numbers are numbers that, other than integers, have a decimal point.
Examples of floating point numbers are

In the "scientific notation", numbers are normalized to one digit left of the decimal point.
A power of 10 is then postfixed to maintain the correct value.
So

^-1

In binary, a number in scientific notation will always have the format 1.xxxxxxx * 2^yyyy
x...x is called the mantissa, y...y is called the exponent.
In the IEEE floating point format, the 1 left of the decimal point is not stored,
but automatically inserted by the processor.

The IEEE standard saves floating point numbers in the normalized scientific notation.
There are two formats:

32 bit

The decimal point (.) is placed left of M₁.
Bit M_n represents the value 2^-n
The M bits together are called "mantissa".

Bit 31 is the sign bit of the mantissa.
If "1" the mantissa is negative, if "0" the mantissa is positive.

Bits E₇ to E₀ make the exponent, which is the power of 2.
A bias value of 127 (binary 01111111) is used, so an exponent of zero is written as 01111111.
Reason is easy comparison of numbers.

Examples

1.
number 8 = 1000 binary
Scientific notation: 1.00000000 * 2³
mantissa = 0 (1. not saved)
exponent = 3, biased exponent = 127 + 3 = 130 = 10000010 binary
The sign bit = 0

floatingpoint number:

0 10000010 00000000000000000000000
2.
number 1/8 = 0.125 = 0.001 binary.
Scientific notation: 1.000000 * 2^-3
exponent = -3, biased exponent 127 - 3 = 124 = 01111100 binary
The sign bit = 0

floating point number:

0 01111100 00000000000000000000000 3.
number 48.7 = 110000.101100110011001101
Scientific notation: 1.10000101100110011001101 * 2⁵
exponent = 5, biased exponent 127 + 5 = 132 = 10000100 binary.
The sign bit = 0

floating point number:

0 10000100 10000101100110011001101

The reason for the exponent bias

Say, we have to compare two numbers: 1 and 1/2
And for the sake of the explanation we use floating point numbers
with a mantissa of 4 bits and also an exponent of 4 bits.

Without exponent bias:

    1 .... 0000 [1] 0000
    1/2... 1111 [1] 0000

note: 1111 (binary) is -1 (decimal) in 2's complement notation.
Comparing the numbers 1 and 1/2 as integers, will result in 1/2 > 1, which is wrong.

Now we use an exponent bias of 0111

    1 .... 0111 [1] 0000
    1/2... 0110 [1] 0000

Now comparing 1 and 1/2 just like integer values clearly shows 1/2 < 1 which is correct.

The reason for an exponent bias is to save circuitry.
Comparison of floating point values can be done by integer compare circuitry.

The 64 bit format

Now, the mantissa is 52 bits long.
Again M₀ = 1 , not saved but added internally by the processor.
The exponent bias is 01111111111
Bit 63 is the sign bit for the mantissa.

In general: converting numbers between different number systems

Say, we have two numbers which have the same value but are written in different number systems:

    aaaa.bbbb
    cccc.dddd

The numbers only can be the same if aaaa = cccc (the integer part) and bbbb = dddd (the fraction part)
So, to convert one number system to another, we separately have to convert
the integer and the fraction part.

Converting decimal integers to binary

We start with the same integers dddd (decimal) and bbbb (binary)
Division by 2: bbbb / 2 = bbb.b ..... the rightmost digit is the remainder of the division.
So also is true: dddd / 2 = ddd.b
Conversion is done by repeated division by 2 while storing the remainders.
We convert 841 to binary

    841 / 2 = 420 r 1
    420 / 2 = 210 r 0
    210 / 2 = 105 r 0
    105 / 2 =  52 r 1
     52 / 2 =  26 r 0
     26 / 2 =  13 r 0
     13 / 2 =   6 r 1
      6 / 2 =   3 r 0
      3 / 2 =   1 r 1
      1 / 2 =   0 r 1

So, [841]₁₀ = [1101001001]₂

Converting decimal fractions to binary

We start with the same fractions .dddd and .bbbb
Multiplying by two: .bbbb * 2 = b.bbbb

So, the leftmost binary digit pops up as integer part.
Conversion is done by repeated multiplication by 2, while storing the integer digits.
We convert .841 to binary

     .841 * 2 = 1.682
     .682 * 2 = 1.364
     .364 * 2 = 0.728
     .728 * 2 = 1.456
     .456 * 2 = 0.912
     .912 * 2 = 1.824
     .824 * 2 = 1.648

So [.841]₁₀ = [.1101011 ]₂ This is an approximation, more digits give a more accurate result.
Note: writing 0.1 decimal will yield an approximation in binary.

Converting binary to decimal

In the binary number b₃ b₂ b₂ b₀ . b_-1 b_-2 b_-3

a binary digit b_n has the value 2ⁿ
Converting binary 101.011 to decimal:

  1--.--- = 4
  -0-.--- = 0
  --1.--- = 1
  ---.0-- = 0
  ---.-1- = 0.25
  ---.--1 = 0.125
  ================
 total      5.375

How the program works

The memory location where a floating point value is stored, is addressed as
an array of bytes.
Then, individual bits of the byte array are extracted and placed in character string s.

Note: byte[0] is located in bits 0..7 of the 32 bit memory word.

type TA = array[0..7] of byte;
     PA = ^TA;

4 bytes are needed for the 32 bit, 8 bytes are needed for the 64 bit floating point number.
PA pointer type points to a byte array.
For the 32 bit format:

var p : PA;
    i,j : byte;
    s,t : string;
    f32 : single;
begin
 s := '';
 try
  f32 := strtofloat(form1.number.text);
  p := PA(@f32);
  for j := 3 downto 0 do
   for i := 7 downto 0 do s := s + chr(((p^[j] shr i) and 1) + ord('0'));
  sign.Caption := s[1];
  t := '';
  for i := 2 to 9 do t := t + s[i];
  exponent.Caption := t;
  t := '';
  for i := 10 to 32 do t := t + s[i];
  coef.Caption := t;
 exept
  ......
 end;

This concludes the description.