In search of weird numbers

download program
download Delphi-7 project

This problem was brought to my attention by mr. Luc Denert, who solved it with pencil and paper.
    a number becomes 11 times smaller when the first digit is moved to the far right position.
    (highest digit becomes lowest digit)
In this article I describe a Delphi program that searches for numbers of the same property with:

- the leftmost digit selectable (1..9)
- the division factor also selectable (2..11)

Find the number that becomes factor smaller if the left most digit is moved right after the number.

In the next description I choose digit 2 as a start and also division by 2.
Multiplication is more simple then division so I changed the problem to:
    a number ends with digit 2 and doubles when this 2 is removed and placed left of it.
Funny about this problem is that it requires only primary school calculation however
even math teachers have problems solving it.
After some erroneous tries one might wonder if such a number anyhow exists.

The algorithm.

Note: a carry is written as (..)

    begin2
    2 x 2 = 442
    2 x 4 = 8842
    2 x 8 = 16(1)6842
    2 x 6 = 12 + 1 = 13(1)36842
    2 x 3 = 6 + 1 = 7736842
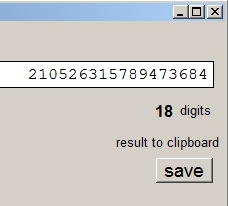
    finally105……...736842
    2 x 1 = 2 2105……..736842
Now the first and the last digits are equal (+ no carry).
Remove the far right 2 and this number is were we searched for.
Next a more revealing picture:



The program


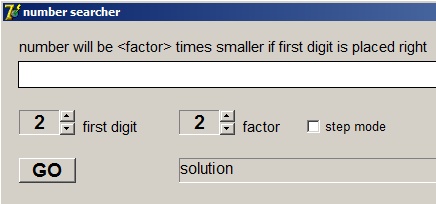
Above we see the program at work..
UpDown controls, associated with statictext components, select the first digit and the multiplication factor.
The GO button starts the search.
The SAVE button copies the result to the clipboard so it can be added to text documents.
If step mode is checked the program shows the intermediate results.
Carries are painted in red.

The number is stored in array A[0…120].
Integer N is index of array A[ ].
Initialization:
N := 0;
A[0] := first digit.

Step 1:
A[N] is multiplied by 2, product to A[N+1] (least significant digit) and A[N+2] (carry).
Step 2:
N := N + 1;
Steps 1 and 2 are repeated until N = 120 (no solution) or A[N] = A[0] and A[N+1] = 0 (no carry).
This code does the work: 
Const maxN = 120;  //maximal number of digits
…..
procedure TForm1.GObtnClick(Sender: TObject);
var carry,i,f,h,N : byte;
    hit : boolean;
begin
 activecontrol := nil;
 for i := 0 to maxN do A[i] := 0;
 displayA(0);
 A[0] := N0upDown.Position;  //starting digit
 f := factorUpdown.Position; //factor
//--
 N := 0;  //array A index
 repeat
  inc(N);
  A[N] := A[N-1]*f + A[N];
  h := 0;
  while A[N+h] >= 10  do   //handle carries
   begin
    carry := A[N+h] div 10;
    A[N+h] := A[N+h] mod 10;
    inc(h);
    A[N+h] := A[n+h] + carry;
   end;
  hit := (A[N] = A[0]) and (h=0);
until (N = maxN) or  hit;
//--
 if hit then begin
              msgText.Caption := 'solution';
              displayA(N);
             end
  else begin
        msgText.Caption := 'no solution';
        label4.Caption := '';
       end;
end;

Step mode

If stepMode is checked intermediate results are displayed.
Mechanism: after each step variable stopFlag is set true.
while stopFlag do application.ProcessMessages;
Pressing the space bar resets the stopflag and the proces continues.
In the form1 object inspector, the keyPreview property must be set "true".
The search starts with :
Activecontrol := nil.
This inhibits that the character is send to the GO button which has focus after being pressed.

Display of array A[ ]

I use a paintbox because digits can be painted in black or red.
The Courier new font has characters with a fixed width.
A[1] is positioned far right.
Variable x holds the character position and x is decremented for each higher digit.
procedure displayA(n : byte); does the work.
n is the number of digits.
A digit (> 0) having a higher position of n is painted in red.

The clipboard

Clipbrd unit is added to the uses clause.
string s holds the result in characters and is place on the clipboard by: 
clipboard.AsText := s;
Every 3 digits a " . " is added to show digits as triples.
Variable p takes care of that.
But first A[ ] must be copied to s, leftmost digit first: 
var s : string;
   i,n,p : byte;
begin
 s := '';
 n := maxN;
 while (A[n] = 0) and (n > 0) do dec(n);//find first non zero digit
 p := 0;
 for  i := n downto 1 do 
  begin
   if p = 3 then begin
                  s := s  + '.';
                  p := 0;
				 end; 
   s := s + char(A[i] + ord('0'));
   inc(p);
  end; 
end;
As mentioned before, this problem for starting digit 1 and division factor 11 was solved by mr. Luc Denert.
He also attended me on a strange property of this number:
Split the number in halves and add them.
The result is 999...99999.

Please refer to the source code for more details.