Delphi use of abs function

Delphi programming techniques

the use of "abs" functions

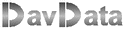Figure 1 below shows a bitmap with rectangle.
The pixels of this rectangle have to be set to the color black.

fig.1

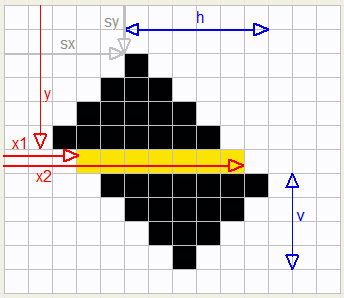
In this article I describe a neat way to do this.
Let us give the top pixel the coordinates (sx,sy).
See figure 2 below. The sides of the rectangle have lengths of h and v.
Say, we are painting the line indicated yellow.
We will accomplish this task by painting a horizontal line from x1 to x2 at y pixels from the top of the bitmap.

fig.2

So, the program will look like this:

var  j : word;
     h,v : word;
     sx,sy : word;
     bm : Tbitmap;
begin
.....
//creation of bitmap
//setting rectangle dimensions h and v
//setting position (sx,sy)
...
 with bm.canvas do
  begin
   pen.color := 0;
   pen.width := 1;
   for j := 0 to h + v - 2     //from top to bottom of rectangle
    begin
     y := sy + j;
     x1 := ???;
     x2 := ???;
     moveto(x1,y);
     lineto(x2,y)
    end;//for j 
  end;//with bm
....  
end;

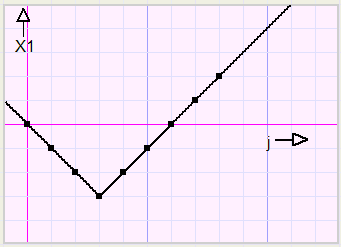
Let's take a look at x1 and it's relation to j.
To simplify the situation we assume that the top pixel has coordinates (0,0).

j	0	1	2	3	4	5	6	7	8
x1	0	-1	-2	-3	-2	-1	0	1	2

Figure 3 shows the graphics

fig.3

This bended line reminds us of the "absolute" function "abs".

fig.4

Above we see the function y = abs(x).

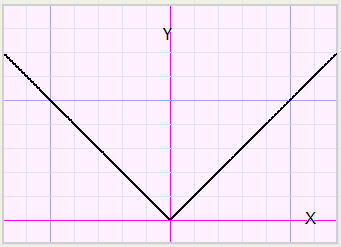
From function theory we know, that if x in a function or equation is replaced by (x-1),
the graph shifts 1 to the right in the coordinate system.
Similar, if y is replaced by (y-1), the graph shifts 1 up
and if y is replaced by (y+1), the graph shifts 1 down.

So, to start with, we consider the function x1 = abs(j).
However, the lowest point is not (0,0) but (3,-3) indicating a right- and downshift of 3.
This changes the function to x1+3 = abs(j-3) or:
x1 = abs(j-3) - 3.

For a height of v the function changes to .............x1 = abs(j+v-1) - (v-1)

Note: moveto(0,0) followed by lineto(10,0) draws a line from (0,0) to (9,0). Pixel (10,0) is not painted.

Finally, sx has to be added, so

x1 = sx + abs(j+v-1) - (v-1) Similar, the function for x2 is ...............x2 = sx - abs(j-h+1) + (h-1)
The proof is left to the reader.

Note: moveto(0,0) followed by lineto(10,0) draws a line from (0,0) to (9,0). Pixel (10,0) is not painted.
So 1 has to be added to X2 if the lineto(..) method is used.