dash-dot line in Delphi

painting dash-dot lines in Delphi

download exerciser program.

download Delphi project.

Introduction

The Delphi programming language has the option to draw dotted lines.
However, only dash-dot lines having a pen width of 1 are possible.
This article describes an efficient method to overcome this limitation.

Painting lines in general

Later in this article we need to paint lines pixel by pixel, dot by dot.
The general function of a line crossing the origin (0,0) of a coordinate system is y = px
where p is the tangent.
In the case of p < 1 the procedure is to step x (0,1,2,3,..) while increasing y by p
and painting a dot at each (x,y) coordinates.
However if p > 1 a problem arises: the line shows holes.

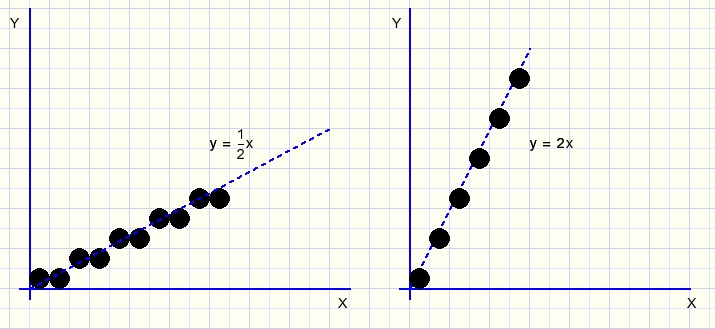
So, if p > 1 the function is rewritten as x = y/p and y is stepped (0,1,2,3,..) while x
is incremented by steps of 1/p.
Considering steps (1,2,3,..) and increment values (p, or 1/p) without wondering which one
applies to x and y, we can focus on simple horizontal lines for the next explanations.

Painting dash-dot lines with a pen width of 1

The dash-dot pattern is coded as bits in a byte and we call this the linepattern.
Painting a dash-dot line amounts to duplicating this pattern by painting a dot for each bit that is set.

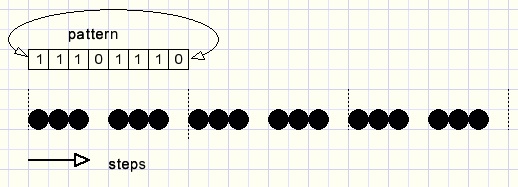
Above is showed a vary much enlarged result.
To find out if a dot must be painted for step N, N mod 8 supplies the pattern bit to be examined for "1".
The value of 8 is choosen on puropse: N mod 8 is calculated simply by N and $7, extracting the least three bits of N.

painting lines with higher penwidths

We apply the same principle as above to paint a line using a pen width of 3.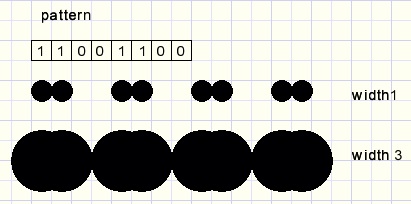

The line - space ratio is completely disturbed.
A way to overcome this problem is to stretch the pattern by the pen width:

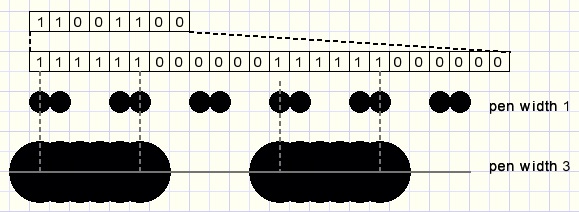
This result is better but not perfect: the empty space to line ratio is less than 1:1
The pen may not overlap empty spaces.
To solve this problem the total width of the pen is considered and dot painting is suppressed if overlap
with an empty space ('0' pattern bit) occurs:

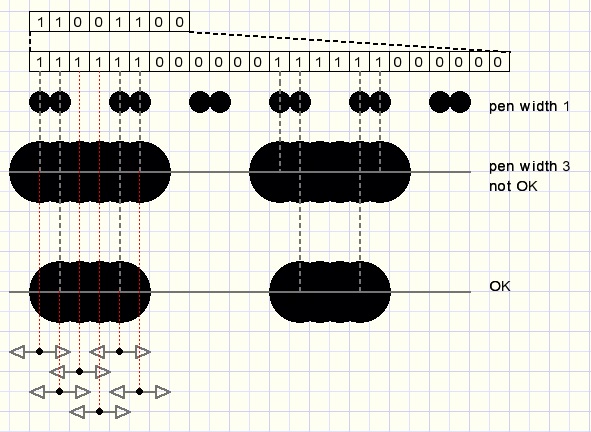
Now the result is fine which raises the question how to program this efficiently,
which means without much time consuming arithmetic operations.

Implementation

Let's consider a penwidth of 5.
The pattern is stretched 5 times, it's size is 5 x 8 = 40 bits.
The pen slides over this expanded pattern with a width of 5.

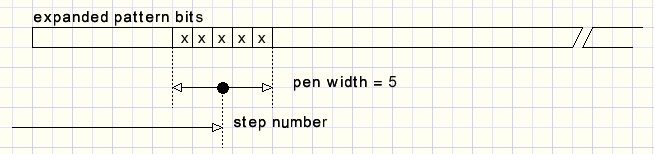
Painting the dot is allowed when the pen does not overlap any '0' pattern bit.

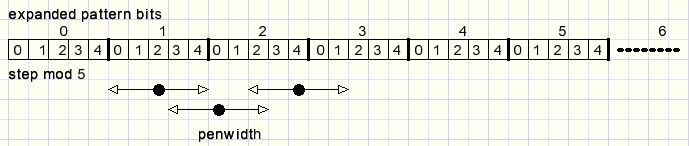
In case of N (mod 5) = 2 then just 1 pattern bit must be checked.
If (N mod 5) = 0,1 the previous pattern bit must be checked as well.
If (N mod 5) = 3,4 the next pattern bit must be checked also.
Numbering the groups of 5 (0,1,2,3,..) we see : group G = N div 5.
The pattern bit P is this group number mod 8, so P = ((N div 5) mod 8)

With 8 pattern bits and a penwidth of 5, after 5 x 8 = 40 steps the situation of step 0 is back,
step 41 needs the same decision as step 1 etcetera.
Knowing the penwidth and the selected dash-dot pattern, an array of boolean may be generated that instantly
shows if a dot has to be painted.

In general, having 8 pattern bits and a penwidth of w we have to calculate the paint decisions for steps 0..5w-1.
In case w is odd:
Counting the pen pixels x from 0..w-1 the middle pixel of the pen is (w-1)/2.
At step N, test pattern bit P = ((N div w) mod 8).
if (N mod w) = (p-1)/2 then this test is enough.
If (N mod w) < (p-1)/2 then also check pattern bit P-1.
If (N mod w) > (p-1)/2 then also check pattern bit P+1.

For even pen widths, a small change is necessary:
Pen pixel position x = w/2 - 1 needs checking of 1 pattern bit.
Again, a smaller x needs checking the previous, a larger x needs checking of the next pattern bit.

Below is a table which puts all patterns with previous, present, next bits together.

 type Tmask = (mp,mc,mn);//previous, center,next
			   
 const maskTable : array[0..7,mp..mn] of byte = 
      (($01,$80,$40),
       ($80,$40,$20),
       ($40,$20,$10),
       ($20,$10,$08),
       ($10,$08,$04),
       ($08,$04,$02).
       ($04,$02,$01),
       ($02,$01,$80);

Following procedure generates the 8*w boolean array DDcheck:

procedure makeDashDotTable(pat,width : byte);
//pat : pattern 
//width : pen width 
//DDcheck[ ] is boolean array for dash-dot paint checking
var   x : byte; //steps 0,1,2,3..
     wx : byte;// 0,1..width-1,0,1,..
   mask : byte;
 center : byte;//for check next,previous p bit 
 begin
  wx := 0;
  center := (w shr 1) - ((w and 1) xor 1);
  for x := 0 to (width shl 3)-1 do
   begin
    m8 := (x div width) and $7;//step mod 8
    with masktable[m8] do
     begin
      mask := mc;
      if wx > center then mask := mask or mn;
      if wx < center then mask := mask or mp;
     end;
    DDcheck[x] := (mask and pat) = mask;  
    inc(wx);
    if wx = width then wx := 0;
   end;//for x
  end;

Some results:

The TXBitmap class

Above procedures are implemeted in my TXBitmap class, which is a TBitmap with many extra options.
The drawing (of all penwidths) is done by copying array FXpen[0..15] of word to the canvas.
FXpen holds a bit coded circle with the diameter of the penwidth.
Changing the penwidth builds a new FXpenwidth array and also builts a new FXddCheck array of boolean.
FddEnd holds the length of the FXddCheck array.
Selecting a new dash-dot pattern also bults a new FXddCheck array.
Now, for line drawing a step counter (ddc) is needed as index to the FXddCheck array.
The following code is the core of line drawing:

//....
//starting x1,y1 values calculated
//increment values dx,dy pre calculated
 ddc := 0;
 for i := 0 to steps do
  begin
   if FXddCheck[ddc] then Dot(x1,y1);
   inc(ddc);
   if ddc = FddEnd then ddc := 0;

   x := x + dx; x1 := trunc(x + 0.5);
   y := y + dy; y1 := trunc(y + 0.5);
  end;

For details I refer to the TXBitmap source code.
An article about all Xbitmap features is found [here].

This concludes the dash-dot line painting explanation.