cyclic redundancy checking

Cyclic Redundancy Codes

goto bit calculator.

Introduction

Cyclic Redundancy Checking (CRC) is a way to insure the integrity of data.
During transmission data may be disturbed by atmospheric interference, bad contacts or other hardware failures.
Also damaged magnetic media cause corrupted data.
Data also may be manipulated by interested parties.

The basic idea of CRC checking is to attach a unique number to the data.
This number is generated in the following way:
Regard the data (message M) as one big binary number.
Choose a number k (called the key) and divide M by k, the remainder is r.
The quotient Q is discarded.
The remainder r is called the checksum and this number is attached to the message,

M = Q.k + r . (Message = quotient times key + remainder)

Look at the next picture for the case of data transmission:

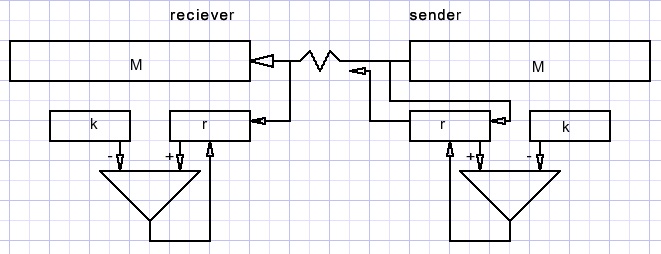
At the sender side, bits of message M send are also shifted into register r while k is subtracted from r.
After message M , the checksum r is transmitted.
At the receiver side also the checksum is generated.
When M bits are transmitted error free, the generated checksum at the receiver side
equals the checksum send by the sender.

Capabilities

In case of a message length of 32 bits and a checksum of 16 bits,
there are 232/216 = 65536 messages that share the same checksum.
This looks bad at first glance but consider a randomly damaged message M:
it only goes undetected if 1 out of 65536 checksums is generated.
With a n bit checksum the chances for a random error staying undetected is 1 / 2n.

Decimal explanation

To understand CRC checking, take the example of normal decimal arithmetic and a key (k) of 10.
Then message 192743 generates a checksum of 3 regardless of the other digits.
Any error except for the last digit 3 goes undetected.
Reason is that 40, 700, 2000, 90000, 100000 are multiples of the key k.
Now consider a key of 11. 192743₁₀ = 1218a1₁₁ {a = 10}
This message will generate a checksum of 1.

Next an error is imposed on M, which becomes 195743₁₀ = 124079₁₁ and now checksum 9 is generated.
The error is detected.

Let our key k be 125.
8 * 125 = 1000 so, errors in digits 3,4,…etc will go undetected
because they impose errors on M that are a multiple of 1000.
Here we reach an important conclusion:
an error E superimposed on message M goes undetected if E is a multiple of k.
Working decimal, 10ⁿ may not be a multiple of k for n = 1,2,3,…..
This is the case when the number system base and the key have no common factors.
With a key of k bits, producing checksums of n = k-1 bits long, any single error burst within n bits will be detected.

Public or secret key?

In the case of data transfers a public key, known by everyone, is fine.
Another situation occurs when CRC checking is used as a signature to protect data
against unauthorized modification.
In this case the checksum is generated with a secret key, only known by the application.

Simplified arithmetic

Before, I mentioned that the checksum is generated by division.
Division implies borrows.
Borrows (and carries) may be avoided by defining addition (subtraction) as exclusive or (xor) operations.
This simplifies hardware without reducing effectiveness.

Binary xor operations are 0+0 = 0; 0+1=1; 1+0=1; 1+1=0;
No carries, no borrows, they are simply ignored.
There is no difference between addition and subtraction.
xor is also called: “logical difference”.

In xor , 0 is the unity element of operation: 1+0 = 1, 0+1 = 1.
1 is it’s own inverse : 1 + 1 = 0.
The associative law holds: (a+b) + c = a + (b+c)
The commutative law holds : a+b = b+a
The distributive law holds: a(b+c) = ab + ac
see the next example as proof where a=1001, b=1100 and c=0111

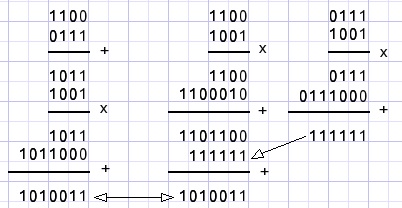
The left column shows a(b+c), the right column ab + ac.
So we have a valid arithmetic system.

Here is another reassuring example:
the calculation a * b / b = a for a=010111 and b=101101

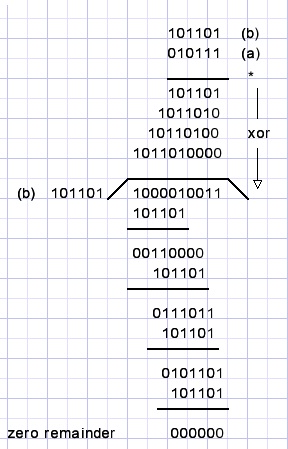
note: we are not interested in the quotient.

Choosing a key

A key of 1 0000 0000₂ will generate checksums that equal the 8 least significant bits
of M because any message of the form xxx 0000 0000 is a multiple of the key.
Any other key is good.
The choice of a key depends on the type of errors expected.
Many keys are designed to detect double bit errors that are far apart.
In that case errors like 100000000000000001 may not be a multiple of the key.
To choose a key may start with factorizing expected errors to make sure they are not a multiple of the key.
This arithmetic, of course, must be performed using the above rules ignoring carries and borrows.

Popular keys

A popular 16 bit key is 1 0001 0000 0010 0001 which is known as the X25 standard.
Another 16 bit key is 1 1000 0000 0000 0101 called the CRC-16 protocol, used in modems.
The Ethernet standard uses the 32 bit key 1 0000 0100 1100 0001 0001 1101 1011 0111

The keys are designed to detect double bit errors that are many bits apart.
Choosing a certain key is based on the assumption that some errors are more likely to occur than others.

Practise

I have programmed an exerciser to perform binary arithmetic.
Carries may be enabled or blocked.
Operations are performed bit by bit at an adjustable speed of 1 to 25 bits per second.

Number may be entered in binary, deximal or hexadecimal form.
Please refer to the link at the top of this page.