

| The distance of diagonals in a cube |
Problem
Find the minimal distance between diagonals AG and BD in the cube below.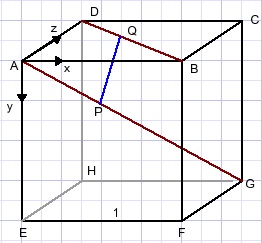
Two solutions are presented:
Numerical
By varying the position of point P on AG and point Q on BD, the minimal distance PQ is found by approximation.
A Delphi program does the job.
Analytical
Straight calculation is used.
The numerical approach.
The positions of P and Q are defined by their (x,y,z) coordinates.
A is the origin (0,0,0).
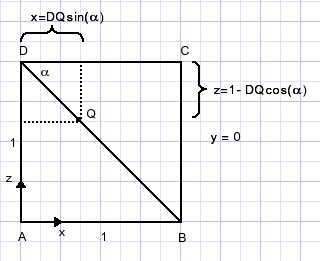
Point Q:
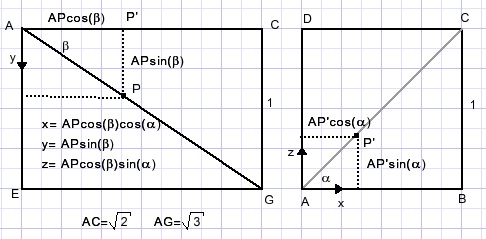
Point P:
Distance PQ:
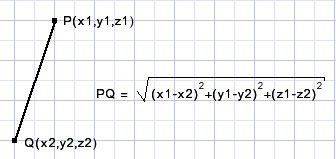
Successive approximation
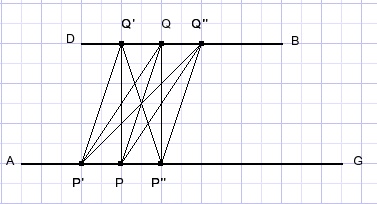
AP'= AP-delta; AP''=AP+delta.
DQ'=DQ-delta; DQ''=DQ+delta.
The initial value of AP=0 , DQ=0, delta=0.1
All distances P'Q', P'Q,….P''Q'' are calculated and the smallest value is saved.
If the smallest PQ was obtained for P'and Q'' then AP is set to AP'and DQ is set to DQ''.
All distances are recalculated with the same value of delta.
If PQ was the smallest distance (so delta=0) then delta is reduced by 50%.
This process repeats until delta becomes very small.
Program description
Pressing the GO button initializes AP,DQ, delta and executes a for loop I := 1..9to calculate the distance between APm, DQm which are the AP, DQ values +/- delta.
The smallest values are stored in LAP, LDQ, Ldistance.
i is stored in mi.
PQ is calculated at i = 5 (no delta value added).
If mi = 5 then delta := delta/2.
The repeat…until loop continues until delta < 0.000001
At form creation time the sine and cosine values are calculated.
(called sina, cosa, sinb, cosb)
The approximation process is recorded in memo1 (Tmemo).
Function floatstring makes a string of double value v with the decimal point aligned.
Function Intstring makes a string of integer value v of fixed length and right alignment.
The string holding the AP,DQ, PQ values is then added to the memo.
The memo1 font is courier new, which has fixed character widths.
The analytical approach
Planes AEGC and DHFB are perpendicular.
So, BD is perpendicular to PQ.
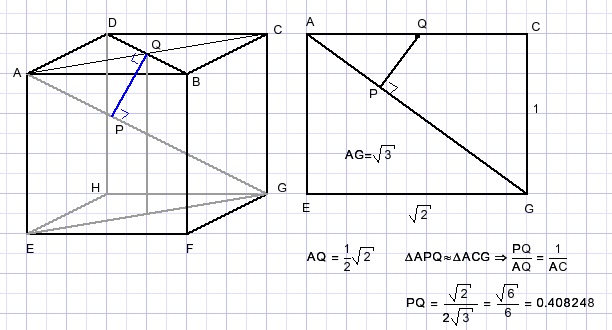
This value is consistent with what was found by the numerical approach.

