combinations

Combinations

Generating combinations

A combination is a choice of elements from a set where the sequence is not important.
Each element may be choosen just once.
An example is the choice of 4 people from a group of 10 to cleanup the room after a party.
When solving a logistic puzzle by brute force, in many cases combinations must be generated in a sequential way.
This is done by assigning a RANK to each combination.
Stepping the rank (0,1,2,3..) and generating the combination then does the job.
For our purpose we use numbers 1,2,3,….,12 as elements.
Example:
4 elements and 2 choices.

Rank   combination
  0	   1,2

  1	   1,3

  2	   1,4

  3	   2,3

  4	   2,4

  5	   3,4

We notice 6 combinations, variable RANK counts 0..5
N : number of elements
K : number of choices
maxRank : number of combinations - 1
below is a picture of the program at work

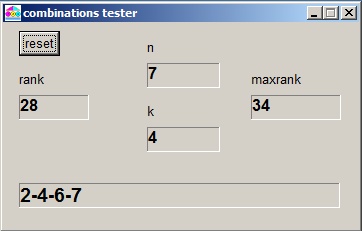
We notice: when choosing 4 elements from a set of 7, rank 28 (of 34) yields 2, 4, 6, 7.

A little theory

Using characters (A.B,C,D) as elements there are 4*3*2*1 = 24 ways to line them up.
Starting ABCD, ending DCBA.
Such a sequence is called a permutation.
Four elements count 4*3*2*1 = 24 permutations.
4*3*2*1 is written 4! and is called 4 faculty.
However: how many permutations are possible with elements AAABCDE ?
If all A's are considered unequal we have 7 elements so 7!= 5040.
The 3 unequal A's have 3! = 6 permutation.
The A's being equal, interchanging A's in a permutation changes nothing.
So there are 3! = 6 times too many permutations.
Elements AAABCDE have 7! / 3! = 840 permutations.
Assume a group of 10 people, we have to choose 4 of them.
To each person a label with character 'Y' or character 'N ' is attached.
'Y' means choosen, 'N ' means not choosen.
The number of choices (combinatios) is the same as how many permutations has YYYYNNNNNN ?.
This is 10!/(4!*6!) = 210, notation C(10,4) = 210.
Trick: first assume all elements unequal, then divide the number of permutations by 4! (characters 'Y'),
then by 6! (characters 'N').
C(n,k) = n! /((n-k)!*k!)

The algorithm

Say we select 3 elements from a set of 6.
There are C(6,3) = 20 combinations, ranked 0..19.

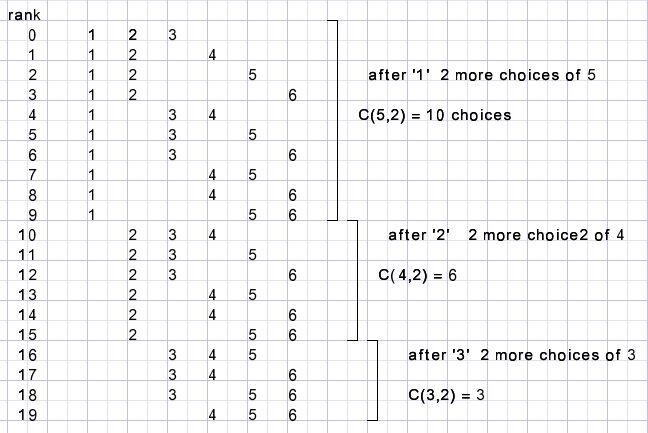
To choose '1 'as first element the rank must be less then 10.
For higher ranks 1 is skipped and the rank is decreased by 10.
Now the rank is 0..9 and '2' is selected if the rank is less then 6, etc.

The program

N, k, rank are displayed in statictext components.
Values may be altered by a left-mousedown (increase) or right-mousedown (decrease).
This function calculates C(n,k):

function CombinationCount(n,k : byte) : word;
//return number of combinations for k choices from n
var d,i : byte;
begin
 result := 1;
 d := 1;
 if k > n-k then k := n-k;
 for i := n-k+1 to n do begin
                         result := (result * i) div d;
                         inc(d);
                        end;
end;

The program combines multiplication and division starting from the lowest values.
This avoids overflows. In case of C(12,6) = 924:
Note: 12!=479001600 The program calculates 7/1 *8/2*9/3*10/4*11/5*12/6
This procedure calculates a combination given the rank:

type TA12 = array[1..12] of byte;

//comdest array holds the choosen elements.

//ep is pointer to the comdest array;

//el is the element number.

.....
procedure Combination(var comdest:TA12; rank: word; n,k: byte);
//calculate combination "rank" of k choices from n elements.
var el,ep,savedk : byte;
    dr : word;
begin
 el := 1;
 ep := 0;
 savedk := k; //save number of choices to make
 repeat
  dr := combinationCount(n-1,k-1);
  if rank < dr then begin
                     inc(ep);
                     dec(k);
                     comdest[ep] := el;
                    end
   else rank := rank - dr;
  dec(n);
  inc(el);
 until ep = savedk;
end;

In the program:
Cn, Ck, Crank values correspond tot the labels Nlabel, Klabel, rankLabel.
The mouseDown events on these labels use a common method.
The labels are tagged 1,2,3 and this tag is copied into the tag of a timer component.
Increasing/decreasing n, k or rank is done by the timer method,
making repeated changes possible while holding the mousebutton down.

Please refer to he source code for more details.