image compression

Image Color compression: an investigation

	download demonstration program
	download Delphi-7 project

Data compression: an investigation

It is nice when the results of research meet our hope and expectations.
However, if the results are disappointing do we have to conclude that we failed?
I don't think so.
Investigation implies that results are uncertain.
Proofing or demonstrating that something does not work also adds to our knowledge.
In this article I present a project that failed.

But before you click away this article, notice that methods are explained to

In an earlier publication I described a project (named SPIC) to compress bitmap images.
One of the steps was the reduction of 24 bit colors to 12 bit.
A 24 bit color code contains 3 fields of 8 bits each for the colors red, green and blue.
This 8 bit value was reduced to 4 bits, making possible 16 shades (0..15) of each basic (r,g,b) color.
For most pictures, 12 bit colors give sufficient quality.
But some pictures with sky and clouds showed light discolorations.

The following idea emerged:
it looks like the human eye is more sensitive to variations of the vivid colors and less to variations of the dark colors.
So why not making a conversion table which provides small steps between the light colors
at the cost of larger steps between the dark colors?

But first I show the color reduction in my old SPIC compression project.
A 24 bits color has 3 fields (red, green,blue) of 8 bits each for the intensity of the base color
This is the conversion table from colorcode to actual color:

code	8 bit color
0	$0f
1	$1f
....	....
$f	$ff

The conversion from color K to code X:

$ff has colorcode $f, $f7 has colorcode $e.

We want smaller steps for the lighter colors so we may choose:
Colors $fc .. $ff have code $f.
$f8 .. $fb have code $e

The treshold value between codes $e and $f is $fc.
To find the treshold values of the other codes we use a quadratic function:

where X is the 4 bits code and K is the 8 bits color treshold.

Starting with 3 pairs (x,K) we may calculate A,B,C .
Table below lists the 3 choices of (x,K) number pairs:

code X	8 bit color K
X1 : 0	K1 : 0
X2 : 10 ($a)	K2 : 198 ($c6)
X3 : 15 ($f)	K3 : 252 ($fc)

For experimentation we need to try different number pairs so at first we calculate a general solution.
The next set of linear equations must be solved: (solve A,B,C)

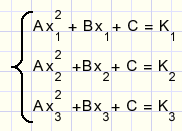
C may be eliminated by the difference between rows:

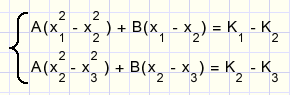
For simplicity we define:

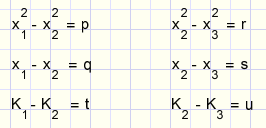
Which provides following set of equations:

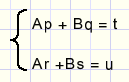
multiplying (*s row 1, *q row 2) :

difference again, division and substitution in previous equations:

This is the plotted function :

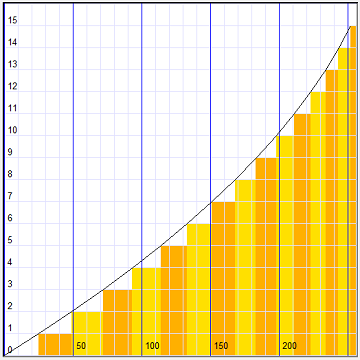
Vertical are color codes X, horizontal are the 8 bit colors K.
We notice that for the higher colors the colored bands are smaller.
These are the treshold values where a code is incremented.
The real color values are between these tresholds, in the middle of the vertical bands.

Starting with colorcode X we may find the treshold color value K by substituting X in the quadratic formula.

But how do we find colorcode X starting with 8 bit color K?
One way would be to apply the ABC formula to solve the quadratic equation: the analytical way.
There also is a numerical way however.
To demonstrate this last method I first give a simple example
we have to guess a number below 16 by asking questions like: “is the number bigger then....”
A (yes/no) answer is 1 bit of information so we need 4 answers to guess a 4 bit (0..15) number.

Two variables do the job, I call them : Base and Step.
K is the number to be guessed (< 16).
Here is the flowchart :

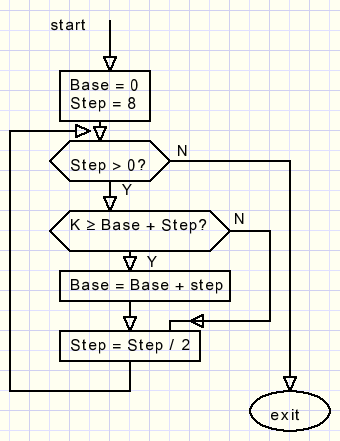
Step divides by 2 after each answer.
After 4 answers Step has value zero and Base is the answer.
Back to our problem we only have to replace the question K >= Base + Step ? by

K>= table[Base + Step] ? That's all.

Now some code of the project.
At first coefficients A,B,C have to be calculated.

procedure makeABC;
var p,q,r,s,t,u : double;
begin
 p := sqr(x1)-sqr(x2);
 q := x1-x2;
 r := sqr(x2)-sqr(x3);
 s := x2-x3;
 t := y1-y2;
 u := y2-y3;
 A := (t*s - u*q)/(p*s - r*q);
 B := (t- A*p)/q;
 C := y1 - A*sqr(x1) - B*x1;
end;

The 3 number pairs are (code,color) : (x1,y1) (x2,y2) and (x3,y3).
S0 x is the code, y is the (treshold) color.
X and Y originate from Tedit components.

Next we produce the table for the treshold values (basevalue[ ]) and also the table for the real colors (penvalue[ ]).
(i is the code)

procedure makebasevalues;
var i : byte;
begin
 for i := 1 to 15 do baseValue[i] := trunc(a*sqr(i) + B*i + C);
 baseValue[0] := 0;
end;

procedure makePenValues;
var i : byte;
begin
 for i:=0 to 14 do 
   penValue[i]:=(baseValue[i]+baseValue[i+1]+3) shr 1;
 penvalue[15] := $ff;
end;

And to find a code from a 8 bit color value: ( x is color, result is code)

function findIndex(x : byte) : byte;
//find closest index in basevalue array for x
var base,step : byte;
begin
 base := 0;
 step := 8;
 repeat
   if x >= basevalue[base+step] then base := base + step;
   step := step shr 1;
 until step = 0;
 result := base; 
end;

The Delphi-7 project has 3 bitmaps:

Also there are 3 paintboxes to show the bitmaps.

Below is pictured in reduced form an example of the project in operation.
Left the original image with 8 bit colors, right after (smart) compression to 4 bits colors and decompression again.
Pictured is the UK escaping just in time from the collapse of the European Union.

I started this article by stating that the results were disappointing.
The demo example below clearly shows so.
Left the original picture, in the middle the simple 4 bit rounding and right the “smart” rounding.

The right picture shows more coarse color steps for the darker colors.
The smaller steps for the lighter colors however are hard to see.

Please refer to the source code for more details.