Cable weights theory and program description

back to help page.
download program
download Delphi-7 project

Contents


introduction to vector calculus
theory
calculations
program description

This article describes the theory and program of the cable-weight project.

This project is a nice application of
    - simple vector calculus
    - Pythagoras lemma
    - basic trigonometry

Vectors

To define a position or a force in a plane requires two numbers.
These numbers are called a vector.
For positions a row vector (x,y) is used.
For forces we use a column vector:



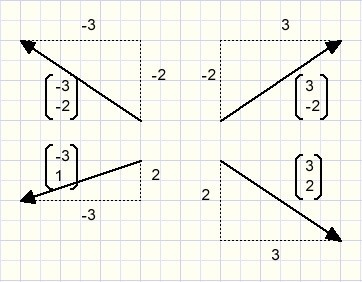
Note: the y direction is positive for the top to bottom direction, just as on the Delphi canvas.

Below are examples of operations on (column) vectors.

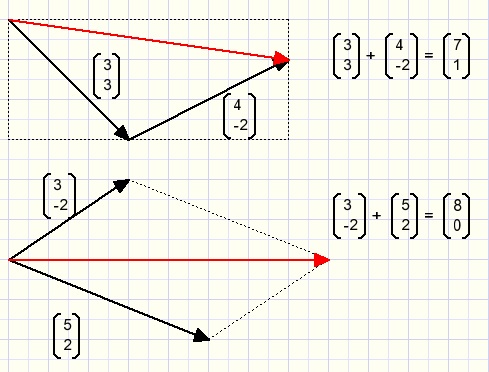
Vector sum
Vectors are connected head-to-tail.



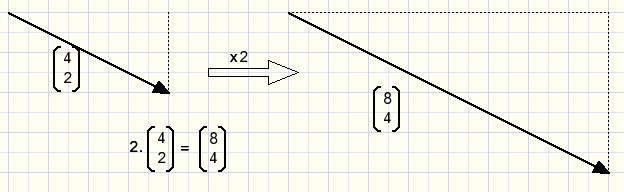
Vector multiplication by a number



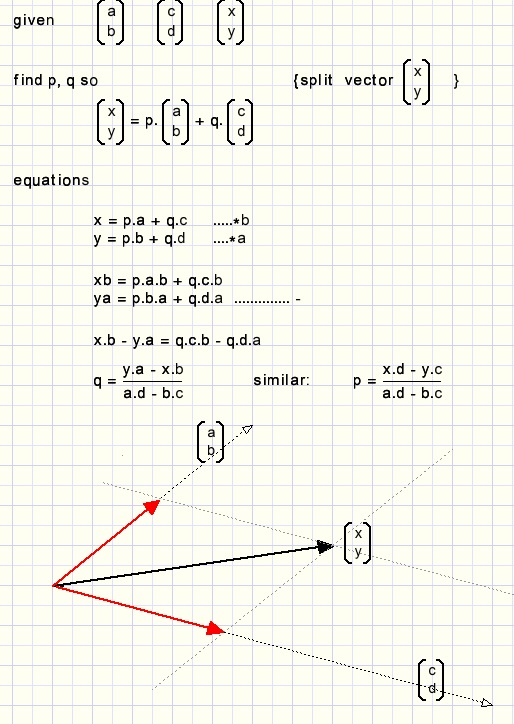
Split vector in given directions



The direction of a vector
(Clockwise rotation for positive angle)



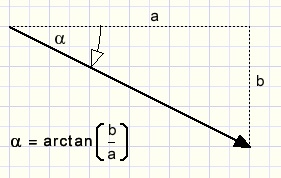
Absolute value of a vector



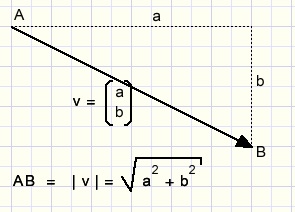
Theory

Objects do not change position if the sum of forces applied to them is zero.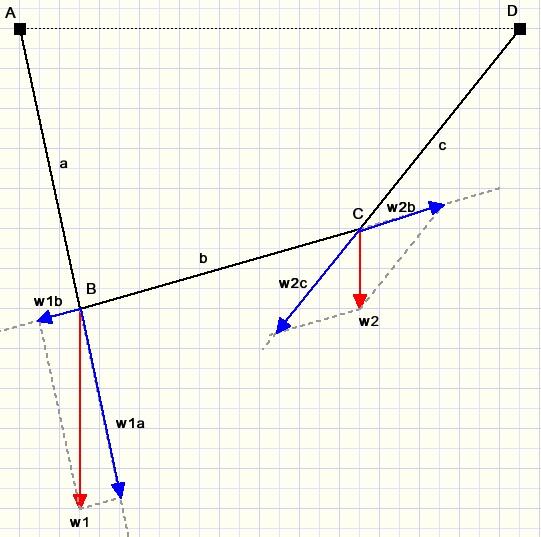



Above is pictured cable ABCD and weights are attached at points B and C.
a,b,c are vectors with direction AB, BC and CD.
In point B 3 forces are active:
    - a downward force w1, the weight
    - w2b, caused by weight 2 at point C
    - an upward force in AB
In point C also 3 forces are active:
    - a downward force w2, the weight
    - w1b, caused by w1 at point B
    - an upward force in CD
Note: AB = a, BC = b, CD = c

Weight vector w1 is split in vectors w1a and w1b with directions AB and BC.
Weight vector w2 is split in vectors w2c and w2b.

Equilibrium is in effect when
    |w1b] = | w1a|

Calculations

Cable lengths AB,BC,CD are given and so are the loads.
The only degree of freedom is the direction of vector a.
Finding the equilibrium is changing the a direction.

First a minimum value of angle A is found.

Finding the minimum value of LA.
Two cases have to be distinguished:



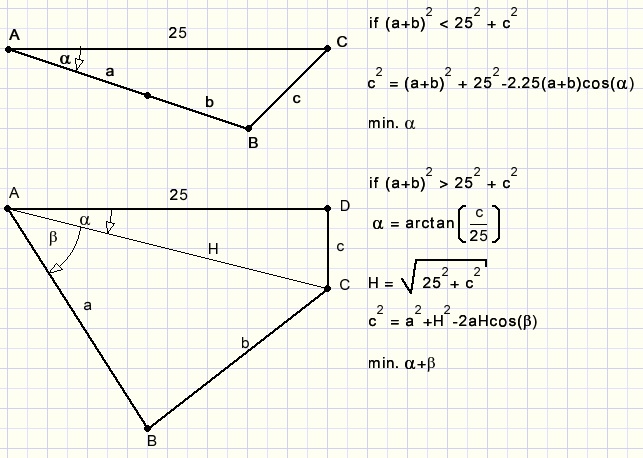
Finding the maximum value of LA



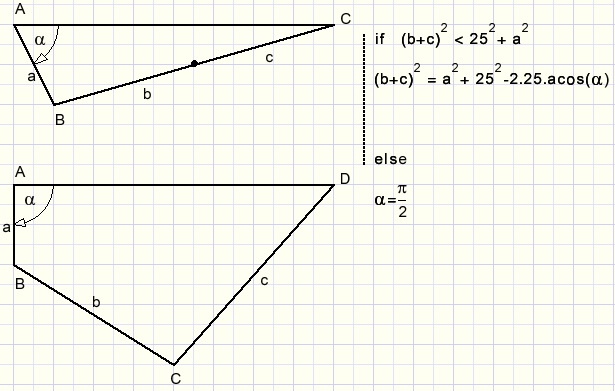
Initially a value minA is set to the minimal LA and maxA is set the the maximal value.
Angle phi = 0.5(minA + maxA) is used to postion vectors a,b,c.
The sum of forces in point B (where weight w1 is attached) is examined.
If a left directed force results, minA = phi.
If a right directed force results, maxA = phi.
This process repeats until no force at point B results.

Constructing the cables from Lphi

This implies direction changes of b, c.

Note: a,b,c are regarded as vectors but also as absolute values.



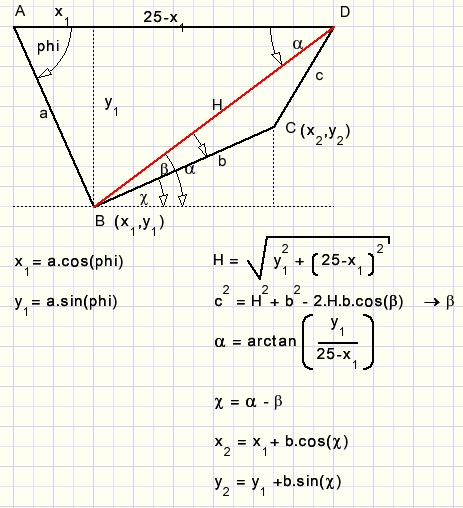
With (x1,y1) and (x2,y2) known, the vectors are easily calculated.

Program description

The Delphi-7 project has one form and one unit.
Painting is done in bitmap map which is copied to paintbox1 on form1.

constants and variables
const maxlinecount = 3;
      maxloadcount = 2;
	  
type TLoad = record
              weight  : byte;
              posX    : double;
              posY    : double;
             end;

     TVector = record
                dx,dy : double;
               end;

var map : TBitmap;
    timercode : byte;
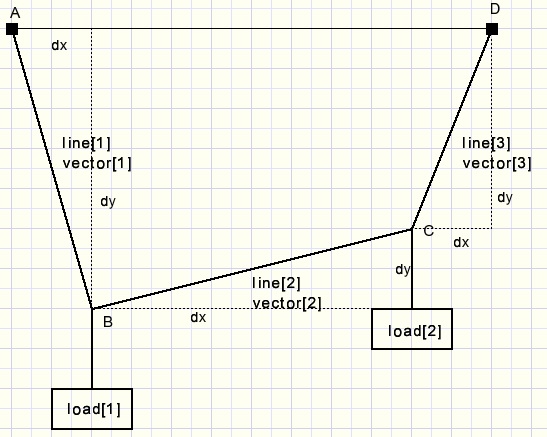
    vector : array[1..maxlinecount] of TVector;
    lines : array[1..maxlinecount] of byte;
    load : array[1..maxloadcount] of TLoad;
    force1 : TVector;
    fline : array[1..3] of double;
    minAngle,maxAngle : double;//lines[1] minimal, maximal angle
    dataOK : boolean;

Variables in action:



Please refer to the source code for paint procedures.
Core of the project is the split vector function
function SplitVector(var v1,v2 :TVector; v3 : Tvector) : boolean;
//call v1,v2 : directions
//return v1 + v2 = v3
var d,f1,f2 : double;
begin
 d := v2.dx*v1.dy - v1.dx*v2.dy;
 if abs(d) < 1e-6 then
  begin
   result := false;
   exit;
  end;
 f1 := (v2.dx*v3.dy - v3.dx*v2.dy)/d;
 f2 := (v3.dx*v1.dy - v1.dx*v3.dy)/d;
 v1.dx := f1*v1.dx;
 v1.dy := f1*v1.dy;
 v2.dx := f2*v2.dx;
 v2.dy := f2*v2.dy;
 result := true;
end;
result is true if calculations were error free.
An error occurs when vectors v1,v2 have the same direction so they
cannot serve as a basis for v3.
On call, vectors v1,v2 are only for the purpose of the direction.
On exit, v1 and v2 are the decomposition of v3, so v3 = v1 + v2 (vector addition, parallellogram)

Other functions / procedures are:
procedure initvectors
Uses the lines[ ] values to calculate minAngle, maxAngle:
the minimal and maximal angles of vector[1]. This procedure calls

procedure makevectors(phi)
which calculates vectors1,2,3 knowing angle phi of vector[1]
and also posX,posY coordinates of the load[1], load[2].

Having set these vectors does not mean that an equilibrium exists.
Therefore procedure newload is called.
This procedure copies minAngle to minA, maxAngle to maxA and then
narrows the range minA..maxA until the resulting forces at point B (where load[1] is attached)
are near zero.
To calculate these forces, procedure calculateForces is called.
A global boolean varible dataOK is true if the splitvector function performed error free.

To change lines and weights, some speedbuttons (+ , -) are added.
These buttons share mouseDown and mouseUp events.
A case statement uses the button tags to recognize the needed action.

For details, please refer to the source code.

This is the end of the cable project description.

Caution
The results have not been verified yet.