Counting binary puzzle solutions

download program
download Delphi project

Sincere thanks to mr. Jelle van der Linde, who supplied questions and information.

Below pictured is a binary puzzle as found in newspapers.
Left is the original puzzle, right is the solved state.



The problem is to fill the empty cells with a 0 or a 1 digit under following restrictions:
    - A row or column may not have more than two consecutive zeros or ones
    - Each row and each column must have an equal amount of ones and zeros
    - No two columns and no two rows may be equal
Binary puzzles come in 4x4, 6x6, 8x8 (as above),10x10, 12x12, 14x14 size.
A good puzzle has only one solution.
Questions are:
    - How to test a puzzle for uniqueness
    - Which digits may be removed in a solved puzzle to preserve a unique solution
    - How many puzzles are possible for a nxn size puzzle?
The last question may be restated as
    - How many solutions has a puzzle with only empty cells?
This Delphi project focusses on the last question.
From here however, answering the other questions requires small steps.
As in many cases, this problem may be approached in an analytical or in a numerical way.

The numerical approach is used.
Take a 6x6 puzzle as example. 6 bits represent a number ranging 0 to 63.
Because of the restrictions, only 14 of these numbers are valid, see below:



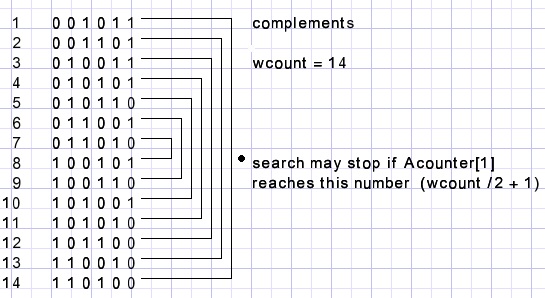
To avoid superfluous work, these valid numbers are generated once and saved in array numbers[1.. ]
Instead of using the 6 bit values, we may refer to rows and columns using the index of the numbers[ ] array.
When filling rows with valid numbers, columns may result with invalid numbers.
So, it is convenient to register per number [0..63] if it represents a valid value.
Array VNlist[number] of Boolean has value true for a valid number.
To generate all possible solutions a counter system is needed.
This counter is called Acounter[1..bitcount ] which holds indexes to the numbers array.
Each element of the Acounter may be considered a digit of number Acounter.



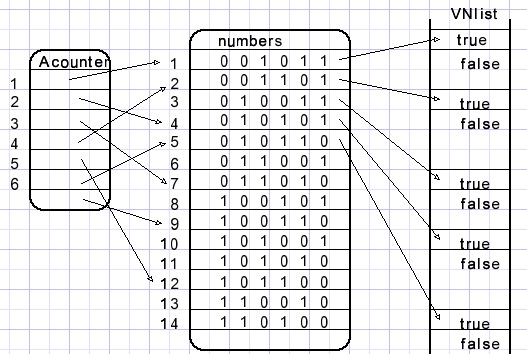
For an nxn puzzle, Acounter has n elements.
The VN list has 2^n elements.
By using the numbers array, all values are valid.

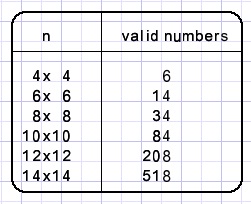
Valid numbers per nxn puzzle



In the selection of a new row, we already may avoid columns with more than two consecutive zeros or ones.
For this purpose there are 
 
Var bitcountmask : word;//2^n - 1; 111111 for a 6x6 game, 11111111 for a 8x8 game
        Amask : array[1..14] of word;
        AFixed : array[1..14] of word;
For row n {n > 2} 
procedure makeFixedbits(n : byte);
var N1,N2,X : word;
begin
 N1 := numbers[Acounter[n-1]];
 N2 := numbers[Acounter[n-2]];
 X := N1 xor N2;
 Amask[n] := x xor bitcountmask;
 AFixed[n] := N1 xor bitcountmask;
end;
Example (6x6 puzzle)



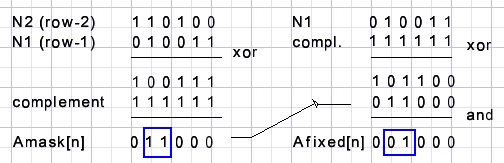
For row n bits 3 , 4 must be 0,1 to avoid 3 consecutive ones or zeros in a column.
When all 6 row numbers are selected these checks must be made
    1. A number may occur only once in the rows
    2. Each column must have an equal amount of ones and zeros
    3. A column may not have three (or more) consecutive ones and zeros
    4. A number may occur only once in the columns
1.
Each new row is compared to the previous rows to avoid reoccurrence.
2.
For the column checks, the columns have to be written as rows which is done by
mirroring over the right top to left bottom diagonal.
This is a time consuming process. So, before writing the columns as rows the rows are summed
and this sum is checked to be (n/2)(2^n - 1) = 189 for 6x6 puzzles.
A 6x6 puzzle has three 1's per column so the sum is 3*(111111)bin = 3*63 = 189.
Only if this test is passed, the columns are written as rows.
3.
A valid column number is simply indicated by the VNlist[number ].
4.
The check for multiple occurrence is done by comparing all numbers.
This row sum check saves 65% of the time for a 8x8 puzzle.
Notice that the row numbers and the solutions appear in complements.
So for each solution there is another one with all cells complemented.
Half the time is saved to count only the first 50% of the numbers in row 1 and counting solutions by
increments of 2. For 8x8 puzzles the number of solutions is counted in 4.3 seconds.
In case of a 10x10 puzzle, about 4 million solutions were counted per minute.
Expected counting time for all solutions is 16 hours.

Results



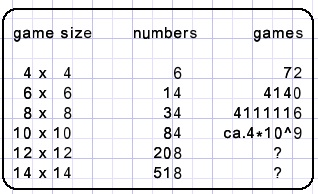
It looks like the number of solutions for empty puzzles increases by a factor 1000 for each next (even) nxn size.

The program




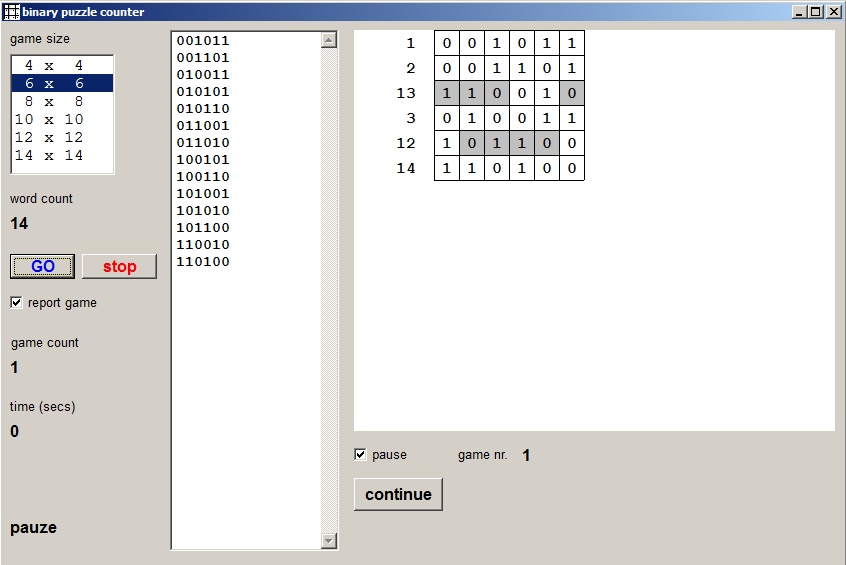
Heart of the program is: 
 
function NextAcount : boolean;
Which updates the Acounter and returns true if a new value is set (no overflow)
Wcount (word count) is the number of valid values in array numbers[].
LInc is a label.
Bitcount = 4 for 4x4 puzzles, 8 for 8x8….
A false exit (end of search) occurs if Acounter[1] updates to a number which has it's MSB set.
This prevents doubling the search time while only counting complements of earlier detected solutions.
A true exit takes place if Acounter[bitcount] is updated without conflict.
This is the flowchart:



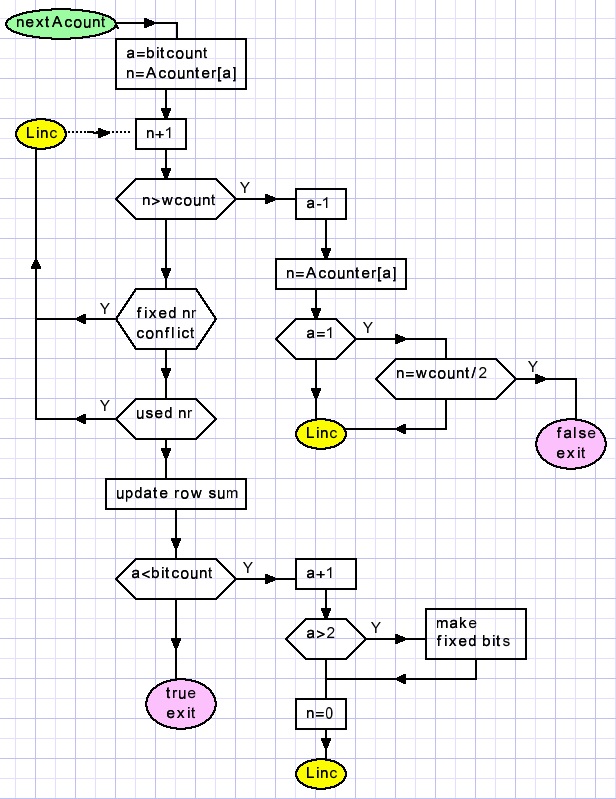
Notice that in this case the use of a label and GOTO statements generates far more readable code
than structured programming using while and repeat statements.

Other functions and procedures: 
function testValid(w : word) : boolean;
Returns true is a number (w) is valid, see restrictions 
procedure MakeNumbers;
Generates the numbers[ ] list and the VNlist[ ]. 
procedure makeFixedbits(ai : byte);
Sets the AMask[ai ] and AFixed[ai ] entries to avoid wrong numbers in a column. 
function UsedWord(a : byte; wix : word) : boolean;
Returns true if index wix not present in Acounter[1..a-1]. Prevents identical rows. 
procedure setGame1;
Called at t the start to supply the 1st game. 
procedure makeVGame;
Transfers columns to rows in array VGame[ ]. 
function checkVGame : boolean;
Returns true if VGame array contains valid numbers.

This concludes the description of the binary puzzle solutions counter.
Please refer to the source code for details.