A simple billiards game

Download billiards program.
Download complete Delphi-7 project.

This article describes a simple billiards game:
the fysics of bouncing balls and a Delphi programming language implementation.



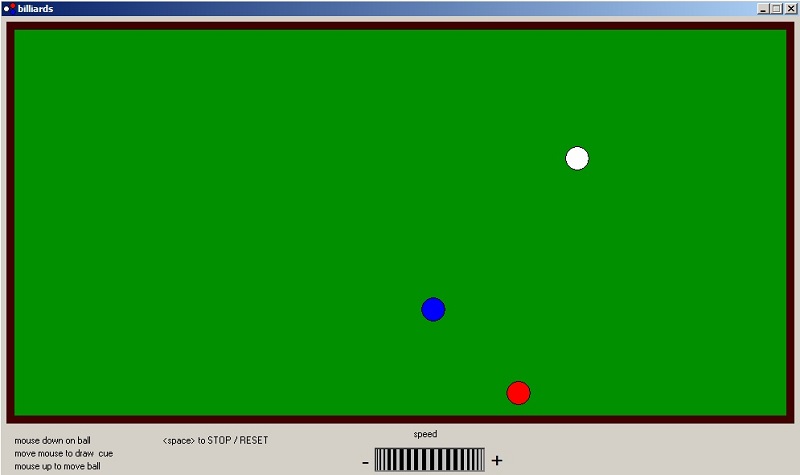
How to use the program

To start a ball movement:
    1. position mousepointer over ball.
    2. press left-mousebutton down and hold.
    3. move mousepointer in opposite ball movement direction (draw cue).
    4. release mousebutton to fire ball.
To stop motion:
    press mousebutton on table
    or
    hit space bar
Pressing the spacebar twice resets the balls to their original position.
To change ball speed:
    press down mousebutton over rotation (speed) button and move mouse left or right.
This project was built to demonstrate ball movement only, not to play billiards.
Once started the balls move forever.
However, it should not be very difficult to make a real billards game:
    1. add the effect of friction, so ball speed decreases.
    2. let the length of the cue define the ball speed.

The fysics of bouncing balls

In the following descriptions we assume "elastic" collisions.
This means that the balls do not change shape.
No energy is lost by deformation or friction, but I confess this is not entirely realistic.

1. Bouncing on edges
When a ball hits an edge, it slightly compresses the point of impact which then
applies a force in the opposite direction of movement.
This makes the ball decellerate first, then accellerating to the original speed but in opposite direction.



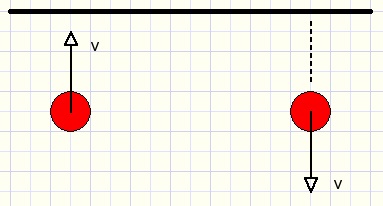
In picture above v is the speed of the ball.
Ball movement is perpendicular to the egde.
For other ball directions, the speed has to be decomposed in a horizontal and a vertical component.
After impact, the new direction is the (vector) sum of the horizontal movement and
the reversed vertical movement.



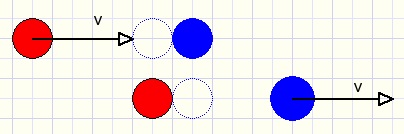
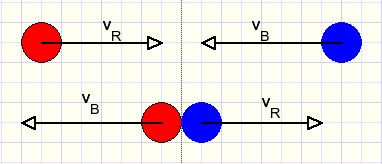
2.Bouncing between balls.
First the situation where only one ball is moving.
In picture below the red ball hits the blue one.
The direction is towards the blue ball center.
The red ball decellerates, the same force however accellerates the blue ball.
After impact, the red ball is in rest and the blue ball continues in the same direction
and with the same speed of the red ball.



Next the situation where both balls are moving towards each others center at different speeds.
Let this speeds be Vr and Vb where Vr = Vb + x.
If x = 0 then the balls bounce and then continue movement in opposite direction.
If the red ball hits the blue one with a speed of x, we saw before that this speed x is passed to the blue ball.
So, in this case after collision, the red ball has a speed of Vb and the blue ball has
a speed of (Vb+x).
A ball simply gets the speed of the other one.



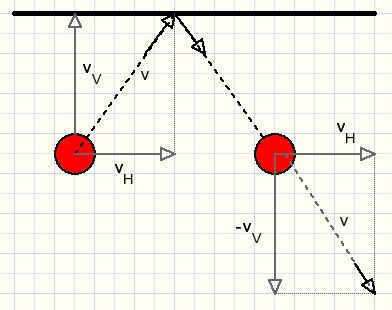
Balls moving in random directions
Ball speeds must be decomposed in speeds in the centerline direction and
perpendicular to this centerline.
Again a ball gets the velocity of the centerline component of the other ball.



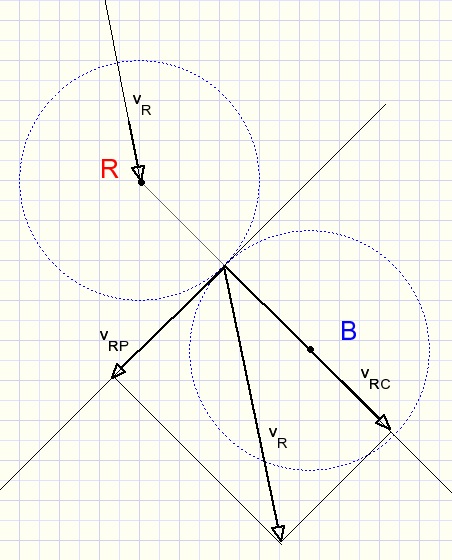
In the above picture only the red ball speed is decomposed for reasons of clarity.
If the blue ball speed is decomposed similarly into components vBC and vBP then
after collision the ball speeds are
    red : vBC + vRP
    blue: vRC + vBP

Direction

The speed always is a positive number.
The direction is in radians so:
    angles from -180...+180 degrees in radians are -p .. +p.
Also note, that in our coordinate system the positive y (vertical) direction is down.
So, in the right bottom quadrant both x and y coordinates are positive.
We apply polar coordinates by defining velocities as a positive value together with the angle of the direction.



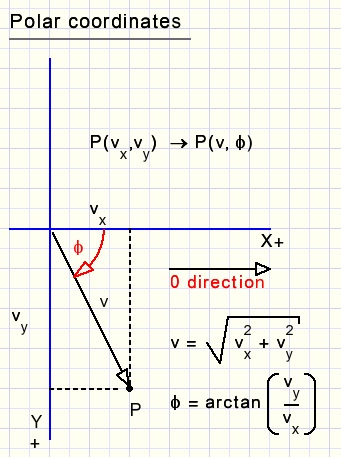
Picture above shows the conversion from a carthesian- to a polar coordinate system.
Decomposing a velocity into two other perpendicular directions is not a problem:



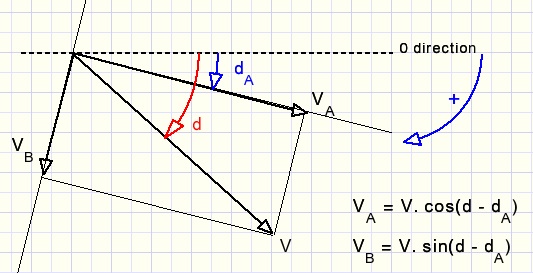
d is the ball movement direction in radians. Angles increase if clockwise rotation.
Other directions do not cause problems or conflicts because the sine and cosine
functions supply the right signs in all quadrants.
One problem remains: the arctan function does not differentiate between diagonally opposite quadrants.
It always returns an angle between -p/2 to p/2



Above, angles are measured in degrees, not radians.
Following function does the work: 
function XYdirection(x,y : single) : single;
//supply direction in radians (-pi .. + pi)
const pi05 = 0.5*pi;
begin
 if x = 0 then
  begin
   if y < 0 then result := -pi05 else result := pi05;
  end
  else begin
        result := arctan(y/x);
        if x < 0 then
         if y < 0 then result := result - pi
          else result := result + pi;
       end;
end;

The program

data formats.
const balldiameter = 30;
      ballradius = balldiameter * 0.5;
      speed = 0.25;  //pixels per step
      pi05 = pi*0.5;
      pi2  = pi*2;

type TBallcolor = (Redball,whiteball,blueball,noBall);
     TBall = record
              xpos : single;  //x coordinate of ball center
              ypos : single;  //y ..
              vel  : single;  //velocity
              dir  : single;  //direction
             end;

var bm : TBitmap;
    ballmap : array[redBall..blueBall] of Tbitmap;
    ball : array[redBall..blueBall] of TBall;
    eraseBall : TBitmap;
    moving,drawing : boolean;
    x1,y1,x2,y2 : smallInt;
    selected : TBallColor;
The bitmap (BM) size is 960*480 pixels, same as paintbox1 on the form.
Edges are drawn on the canvas of the form, around the paintbox.

Balls are separate transparent bitmaps which image is painted at creation time.
The eraseMap is a bitmap with green canvas to erase balls.

Accuracy

A ball always starts with a speed of 0.25 (pixel per update).
This is the maximum value.
Ball positions are advanced step by step.
After each step checks are made for any overlap between a ball and edge or another ball.
Small steps will yield a higher accuracy, a more precise point of impact.
After 8 increments the screen is updated by
    1. erasing the balls
    2. painting the balls at new positions
    3. copying the bitmap (bm) to the paintbox.

Timing

The computer has a milliseconds counter: function gettickcount
returns the number of milliseconds since the computer was switched on.
However, this clock value is updated only at about 16 milliseconds intervals which is too slow.

Another clock runs at CPU clock speed.
This is the one we use.
Processors have different clock speeds so a conversion is needed from CPU ticks to real time.
This is done by procedure GetCPUticks which returns the number of clock ticks per microsecond.
Function CPUtime returns the number of clock ticks in a 64 bit integer since the computer was switched on.

To allow for fast or slow ball movement a rotation button is created under the billiard table.
This button is a home brew component but to make things easy for my readers
I have added the code as a separate unit and I create the button at the start.
No need to install foreign components.

The position value of the rotation button runs from 0 to 100.
This value is used to control ball speed.



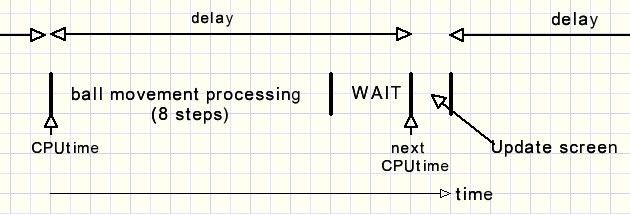
Ball movement processing takes about 500microseconds for 8 steps. (if 3Ghz clock)
Delay values range from 1000 to 10000 microcesonds.
Increments of the delay value are relative, not absolute.



100 - buttonposition because a higher value must yield a lower delay time.
variable nextCPUtime = CPUtime + CPUticks * delay.

Ball movement

At each step, the ball positions are advanced by the value of their velocity.
After that a check is made to see if an edge was hit.
Then checks are made for collision : red/white, red/blue, white/blue.
Procedure collision(a,b : TBallColor) checks and processes ball movement for collisions.

meaning of variables in procedure collision(a,b : TBallcolor)
xAball a X coordinate
yAball a Y coordinate
xB,yBball b similar...
dAball a direction
vAball a velocity, always positive
dB,vBball b similar...
ddistance between centers of balls a,b
dCCdirection of line between centers of balls
vACball a centerline component velocity (+ or -)
vAPball a velocity of component perpendicular to center line (+ or -)
vBC,vBPball b similar...

For details I refer to the theory above and the source code.