algebra problem

Algebra problem (5)

This problem can be solved in two ways:

1.
A somewhat intuitive approach.
We notice whole numbers.
This implies that a,b,c cannot be a fraction.
But a,b,c cannot be all integer either.
The sum of squares shows that the absolute value of a,b,c is 3 or less.

Squaring the root of an integer results in an integer.
In rows 1 and 3 above the root terms must cancel each other.

What rests is a format like

where x,y,z are integers.

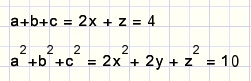
So, we can write the next equations:

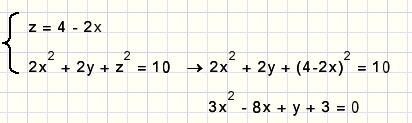
Let's consider y+3 a constant.
The ABC rule yields

If y = 1 then x = 2 and a = 1, b = 0, c = 3.
This is incorrect as it results in a wrong value for the sum of 3rd powers.
Take y = 2.
Now x = 1 and z = 2. (select integer value)

Now we notice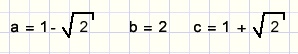

Substituted in row 3 above:

This is a correct solution.
Substituted in row 4:

2.
A solution without calculating the individual values of a,b,c.
We try to write a⁴ + b⁴ + c⁴ as a formula of row 1..3 values.

First however a consideration that saves a lot of work.
This is a symmetrical problem.
a,b and c my trade positions without affecting the answer.
While writing (a+b+c)⁴ as the sum of terms all combinations of 4 letters (a,b,c) will occur.
However many terms are equal such as aaab, abaa, aaba.
Combinatorics learns us the number of equal terms.
Four different factors (as abcd) may be written in 4! = 24 sequences.
However, if 3 factors are equal (as in ab³) then 24 must be divided by 6 ,
because 3 factors may be written in 3! = 6 sequences which make no difference.
So, term a²b² occurs 24/(2!2!) = 6 times.
abc² will occur 24/(1!1!2!) = 12 times.

Let's go:

Now the next:

note: we wrote 6abc = 9abc - 3abc

Continuing:

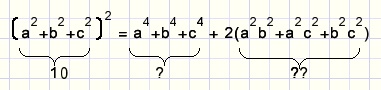
Here the answer shows up at ? but what to do with ??

Combining the above results: