

| Algebra problem (45) |
Problem
This problem was posted by Lahcene Belhadj in Facebook group "Classical Mathematics".The solution is my own.
Calculate:
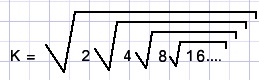
Solution
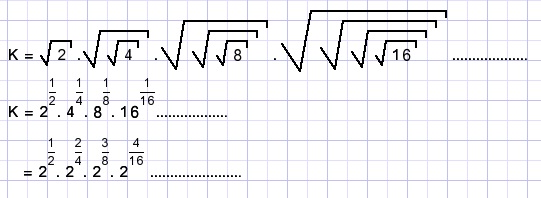
let:
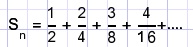
calculate Sn for n = 1, 2 3, 4, .....
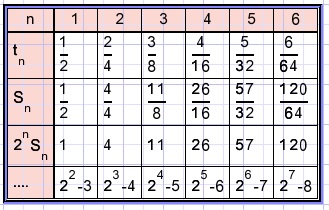
and we see
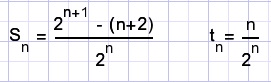
which is certainly correct for n=1 to n=6 but further?
To obtain general integrity we need to prove that Sn+1 = Sn + tn+1.
Because if Sn is true for n=1 than also for n=2,3,....

It works!
What happens to Sn if n grows very large?
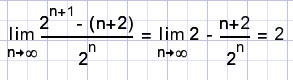
so K = 22 = 4.

