Algebra problem (4)

This great algebra/geometry problem was found in FaceBook group "Geometria".
It was posted by Angel Silva Palacios.

Picture below shows a square with inside a point P such that:
    c2 = a2 + 2 b2


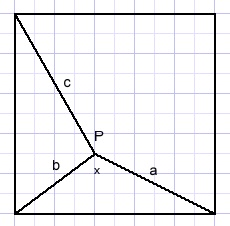
Question: calculate angle x.

Solution

Say the edge of the square is 1.
Let the coordinates of P be P(x,y).{different x, not the angle}
The origin (0,0) is the left bottom corner.



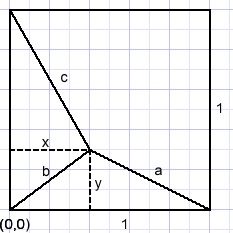
Apply the Pythagoras lemma for lines a,b,c:
    a2 = (1-x)2 + y2
    b2 = x2 + y2
    c2 = x2 + (1-y)2
Now subsitute these in c2 = a2 + 2 b2 :
    x2 + (1-y)2 = (1-x)2 + y2 + 2(x2 + y2)
    remove parenthesis:
    1 - 2y + y2 + x2 = 1 - 2x + x2 + y2 + 2x2 + 2y2
    simplify:
    x2 + y2 + y - x = 0.
This equation represents a circle with center other than (0,0).
Rewriting:
    x2 -x + 0.25 + y2 + y + 0.25 = 0.5.
    writing the square root of 2 as sqrt(2) then:
    (x - 0.5)2 + (y + 0.5)2 = sqrt(0.5)2
This is a circle with radius sqrt(0.5) and center (0.5 , -0.5)



As we see, the angle x spans an arc of 2700 so:
    x = 1350