

| Algebra problem (26) |
This problem was placed on LinkedIn group "Math Education" by DEB JYOTI MITRA.
A right angled triangle has a perimeter of 30 (meter) and an area of 30 (meter2).
Calculate the lengths of the sides.
Some guessing with Pythagorean triples :
(5, 12, 13) because
5 + 12 + 13 = 30 but also
5.12/2 = 30
How to perform the calculation?
Say the right angled sides have lengths a and b, the hypothenuse is c.
The following system of equations has to be solved:
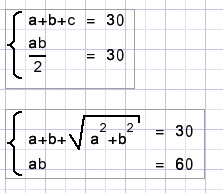
Problem is the root.
The tric is how to eliminate the root.
Solution 1
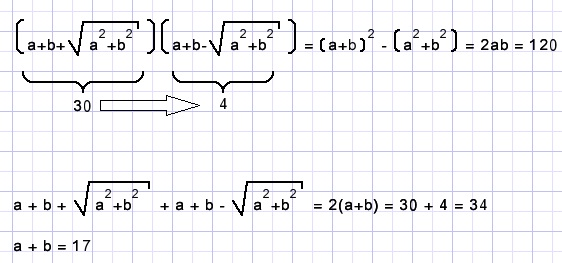
Equation ab = 60 becomes
a(17-a) = 60
a2 - 17a + 60 = 0.
ABC rule:

a1 = 5
a2 = 12
The sides have lengths of 5, 12 and 13.
Solution 2
(a+b)2 = a2 + 2ab + b22ab = 120
c = 30 - (a+b)
(a+b)2 = 120 + (30 - (a+b))2
(a+b)2 = 120 + 900 -60(a+b) + (a+b)2
60(a+b) = 1020
a+b = 17
ab= 60 now becomes
a2 - 17a + 60 = 0.
Factorization:
(a-5)(a-12) = 0
The rigth angled sides have lengths of 5 and 12, the hypothenuse is 13.

