

| Algebra problem (25) |
If
a + b + c = 1 and
a3 + b3 + c3 = 4
calculate

Solution
First, (a+b+c)3 is calculated
Problem are the denominators a+bc, b+ac, c + ab.
Addition causes excess work.
How to avoid this misery?
(1-a)(1-b) = 1-a-b+ab
however 1-a-b = c so
(1-a)(1-b) = c + ab
Similar we may write:
(1-a)(1-c) = b + ac en
(1-b)(1-c) = a + bc
which makes
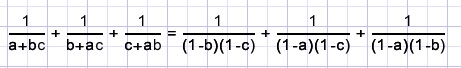
Addition of the fractions now is simple:
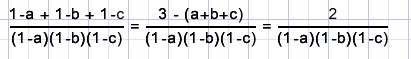
The numerator is found, next the denominator.

The answer is 2/(-1) = -2.

