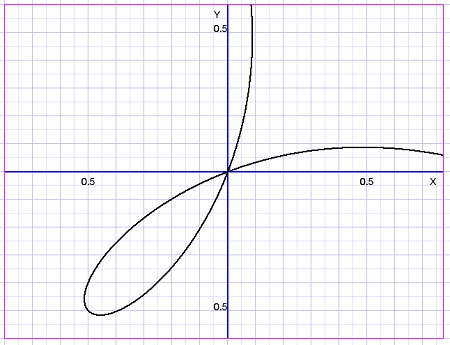
Algebra problem (17) Given is a curve with equation: x3 + y3 - x2 - y2 + 3xy = 0 Question: calculate the derivative (tangent) in point (0,0). This is a so called implicit function which have the general form: f(x,y) = 0. This is the graphical representation: Differentiation yields: 3x2+3y2y'-2x-2yy'+3y+3xy'=0 For point (0,0) we see 0 = 0. This doesn't really help. We draw a straight line (y = ax) through (0,0) and calculate the intersection with the curve. For y we substitute ax : x3 + (ax)3 - x2 - (ax)2 + 3ax2 = 0. x2[x(1 + a3 ) - 1 - a2+3a] = 0 Or x2 = 0, x = 0 Or x(1 + a3 ) - 1 - a2+3a] = 0. 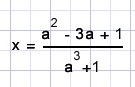The straight line may only intersect the curve at (0,0) so x = 0 must be true. a2 - 3a + 1 = 0. 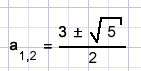ABC rule for solving quadratic equations: is the answer. Parametric functions From here it is a small step to write the equation in parametric form. The general parametric form is: y = f(t) x = g(t) Both x and y are function of an interim variable, mostly called t. But here we see a, the tangent. 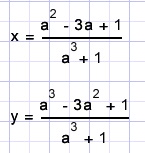Because y = ax we may write Let a run from -50 to +50 in many small steps, calculating (x,y) for each step. Now, drawing the curve is much faster then in the case of the implicit form, where each (x,y) point in the coordinate system has to be examined for position on the curve.