Algebra problem (12)

In the Omid Motahed "Classical Mathematics" Facebook group, problems related to mathematical analysis,
number theory, geometry and math computer software are discussed.

Another superb problem was spotted here recently, together with 3 amazing solutions.
So please read on.

The problem (by Tilikraj Kaushal)
given:
    x2 + y2 + xy = 9
    x2 + z2 + xz = 16
    y2 + z2 + yz = 25
Question
    xy + xz + yz = ?
solution 1 (Bikiran Das)
solution 2 (Paul Christian Abbott)
solution 3 (Dr. Kevin Wang)


I have entered hand written texts in my (DavDoc) math editor.
An additional explanation was added to solution 3.

Solution 1.

(Bikiran Das)



Solution 2.

(Paul Christian Abbott)

Since the problem is homogenous, a simple general approach is to write
    y = ax
    z = bx
Then the 3 equations read



Solution 3.

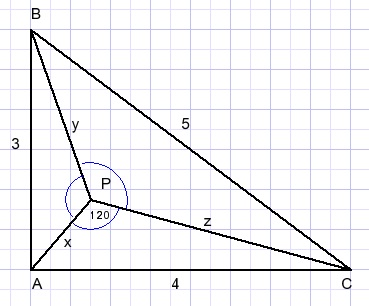
(Dr. Kevin Wang)

In a certain triangle ABC, let P be the Fermat point
(i.e. the angles APB=BPC=CPA=120 degrees)
Let x=AP, y=BP, z=CP.
Then according to the given equations (which are the law of cosines)
    AB=3
    AC=4
    BC=5
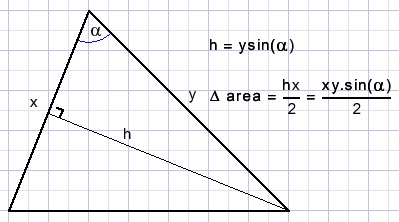
So this is a right triangle with area 6.
The area can also be expressed as



Explanation of solution 3



The cosine rule applied to ΔAPB
    32 = x2 + y2 - 2xycos(120)
    since -2cos(120) = 1
    x2 + y2 + xy = 9
    etc.
The area of a triangle expressed as 2 sides and their angle: