| Algebra problem answers (70..76) |
70.
A.
x,y,z are positive integers.
3x = 4y = 5z
Calculate the smallest possible value of x + y + z.
Solution A.
Let 3x = 4y = 5z = K, so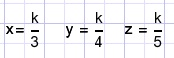
then:
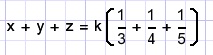
because LCM(3,4,5) = 60
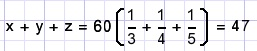
B.
x + y = y + z = x + z = xyz.
Calculate x,y,z.
Solution B.
x = y = zso:
-
2x = x3
x(x2-2)=0
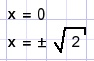
C.
x + y + z = 0
x2 + y2 + z2 = 14
x3 + y3 + z3 = 18
Question:
xyz = ?
x,y,z = ?
Solution C
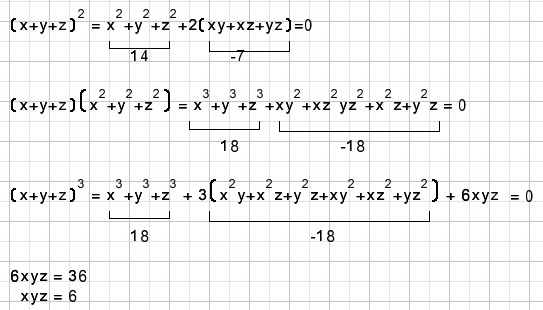
To calculate each x,y,z it is convenient to describe them as solutions of an equation
-
(t-x)(t-y)(t-z) = 0
so
t3 - t2(x+y+z) + t(xy + xz + xz) - xyz = 0.
Because (calculated before) x+y+z =0 and xy+xz+yz=-7 and xyz=6 .....
t3 - 7t - 6 = 0
(t+1)(t-2)(t-3) = 0
x = -1
y = -2
z = 3
D.

Note: bereken = calculate.
Solution D.
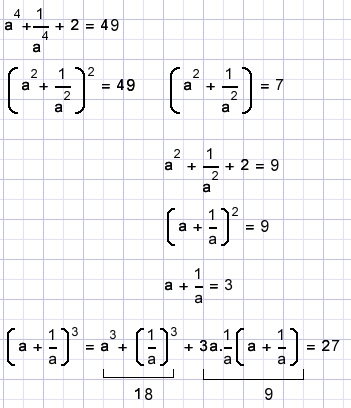
71.
A.
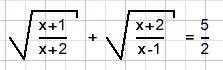
x = ?
Solution A.
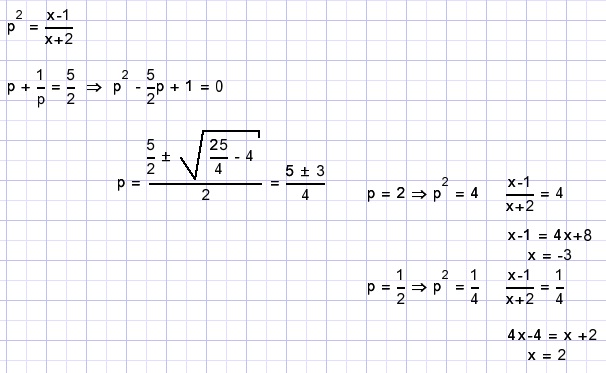
B.
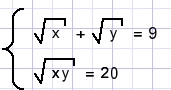
x=?
Solution B.
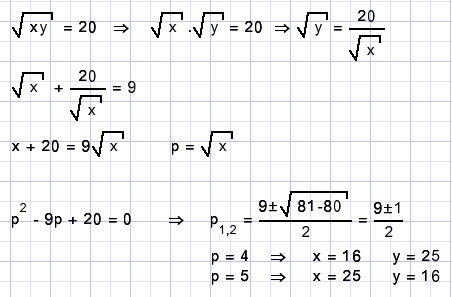
C.
x=?
Solution C.
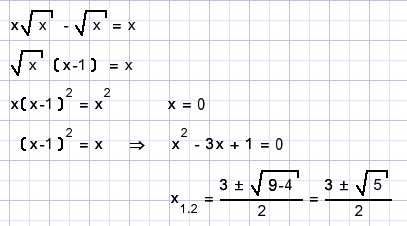
D.
9x + 9x = 9
31-x = ?
Solution D.
2.32x = 9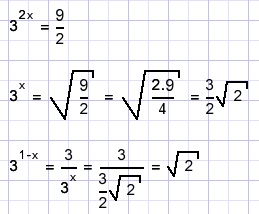
72.
A.
Calculate x if
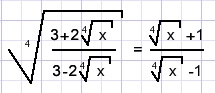
Solution A.
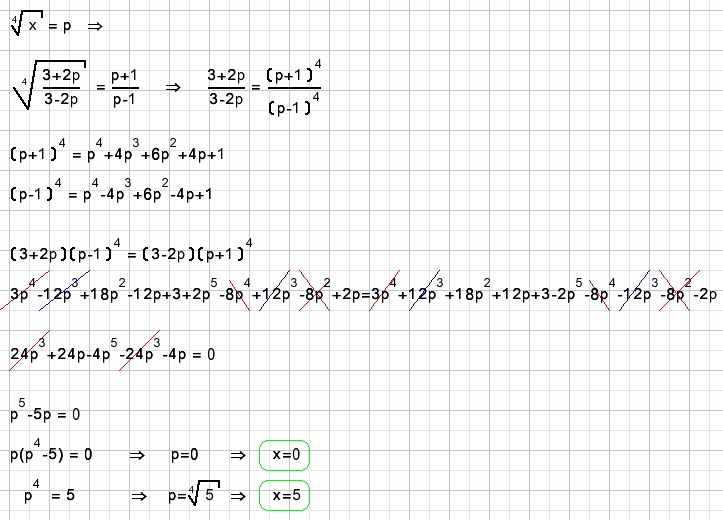
B.
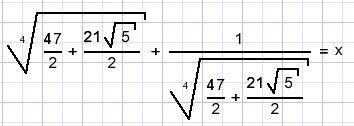
Calculate x.
Solution B.
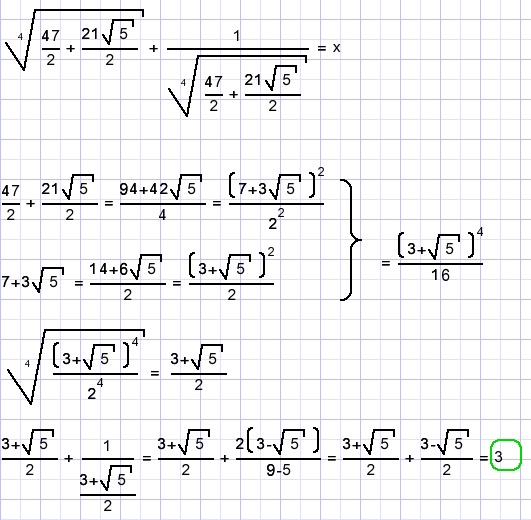
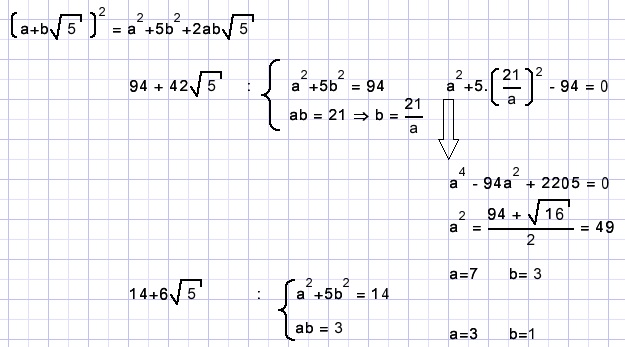
Explanation
C.
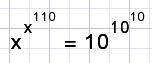
Calculate x.
Solution C.
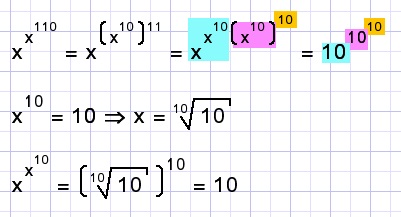
73.
A.
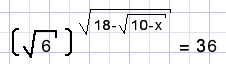
x = ?
Solution A.
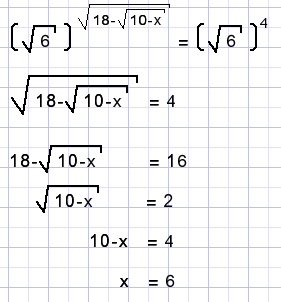
B.
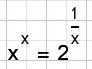
x=?
Solution B.
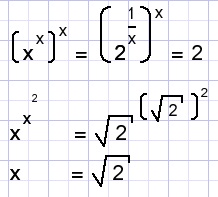
C.
a4 + b4 = a2 - 2a2b2 + 6.
a2 + b2 = ?
Solution C.
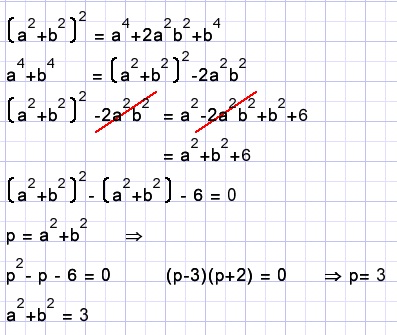
D.
(a2+1)(b2+1) + 25 = 10(a+b).
a3 + b3 = ?
Solution D.
We notice two unknowns but only one equation.This is possible only if there are two squares that both are zero.
Remember: if A2 + B2 = 0 then A=0 and B=0 .

E.
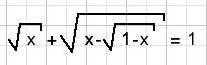
x=?
Solution E.
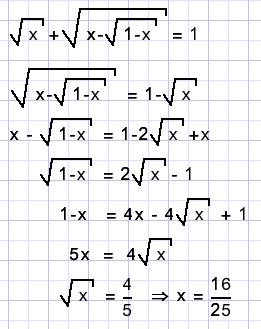
F.
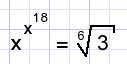
x=?
Solution F.
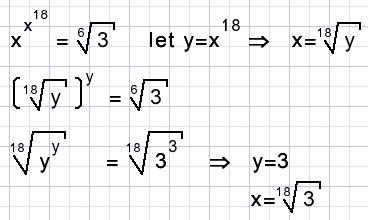
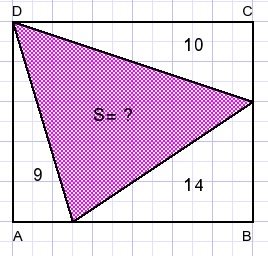
74.
Given is rectangle ABCD and some areas of right angled triangles within.
Calculate area S of the shaded triangle.
Solution
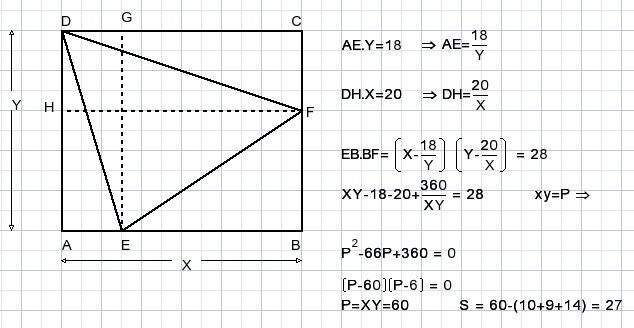
Note: each fact is used once to form an equation.
75.
A.
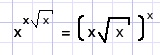
x=?
Solution A.
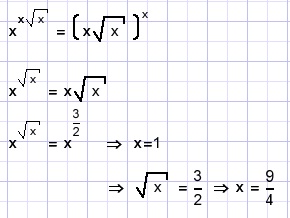
B.
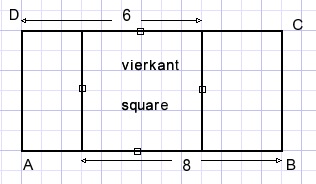
Perimeter of ABCD = ?
Solution B.
Let AD=a
6-a+8+a+8-a+6+a=28
C.

Solution C.

D.
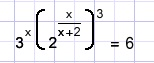
x=?
Solution D.
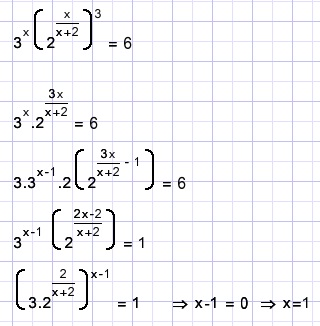
E.
x and y are positive integers.
x + xy + y = 54.
x=? , y=?
Solution E.
Let y=x+p.x2+x(p+2)+p-54=0
discriminant = (p+2)2-4(p-54) must be square.
p2 + 220 must be square, OK for p=6.
x=4
y=10
76.
A.

Solution A.
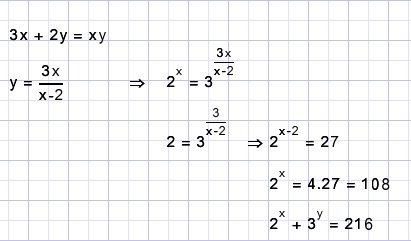
B.
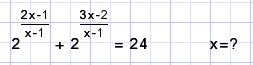
Solution B.
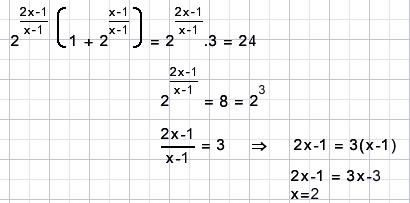
C.
a,b,c are integers.

Solution C.
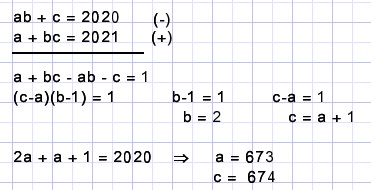
D.
9x-6x=4x.
x=?
Solution D.