

| Algebra problem solutions (60..69) |
60.
| solve | 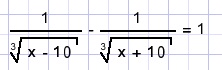 |
Solution
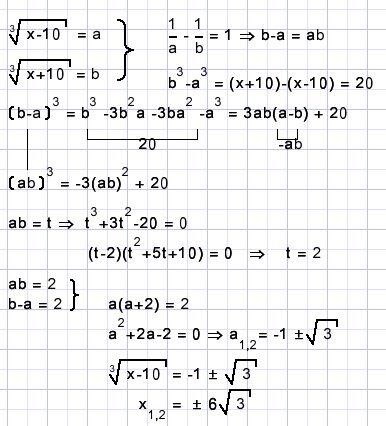
61.
A.
| find n if | 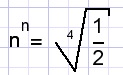 |
Solution
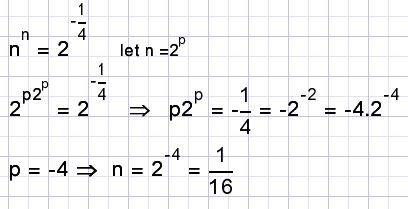
B.
| calculate n if | 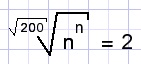 |
Solution
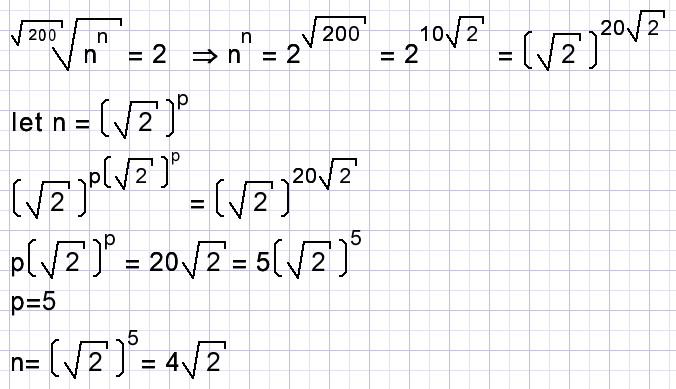
62.
| calculate | if |
Solution
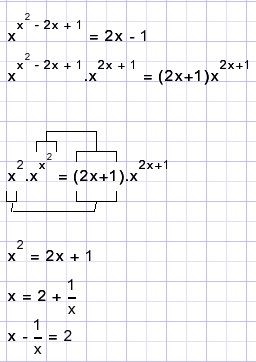
63.
2n + 2n-1 = 48
Calculate n.
Solution
2.2n-1 + 2.n-1 = 483.2n-1 = 48
2n-1 = 16 = 24
n -1 = 4
n = 5
64.
x3 + x2 = 392.
Calculate x.
Solution
x2(x+1) = 23.72x2(x+1) = (7+1).72
x = 7
65.
| If | 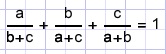 |
calculate | 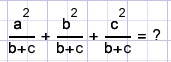
|
Solution
Successively multiply by a, b, c and add :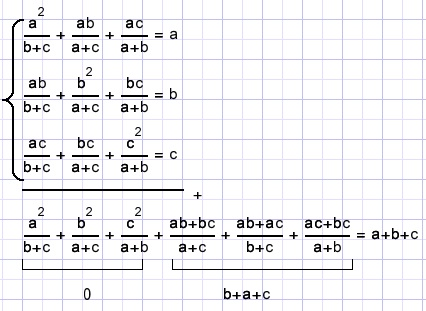
66.
A.
n is a positive integer.
| Prove that | 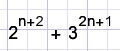 | is divisible by 7 |
Solution
This is a proof based on induction.Assume that the formula is correct for some value of n.
Then prove that the formula would also be true if n is replaced by (n+1):

The formula is OK for n=1.
So also for n=2,3,4,......
B.
N is a positive integer.
| Prove that the fraction |  | is not reducable for any N |
Solution
Note: GCD(A,B) means the greatest common divisor of A and B.We use the Euclides lemma stating that GCD(A,B) = GCD(A-B,B).
GCD(21N+4,14N+3)=GCD(7N+1,14N+3)=GCD(14N+3,7N+1)=
GCD(7N+2,7N+1)=GCD(1,7N+1)=1
There are no common factors, the fraction cannot be reduced.
C.
x and y are integers.
Prove that :
-
if 2x + 3y is divisible by 17 than also 9x + 5y is divisible by 17.
Solution

67.
A.
x4 + x2 = 90.
Calculate x3
Solution
Let p=x2p2 + p - 90 = 0
(p+10)(p-9)=0
p=9
x=3
x3 = 27.
B.
8n = 27.
Calculate 4n.
Solution
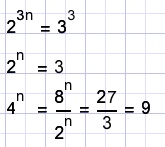
C.
32x+1 + 3 = 3x+2 + 3x.
Calculate x.
Solution
3.32x + 3 = 9.3x + 3x.Let 3x = p.
3p2 + 3 = 10p.
3p2 - 10p + 3 = 0.
(3p-1)(p-3) = 0.
3p-1=0; p=1/3; x = -1.
p-3=0; p=3; x = 1.
D.
| simplify | 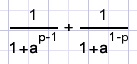 |
Solution
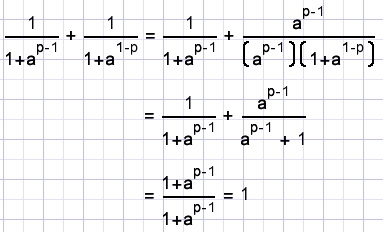
E.
2x-3y=4
| calculate |
Solution
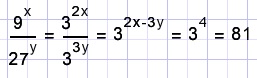
F.
| solve x op |  |
Solution
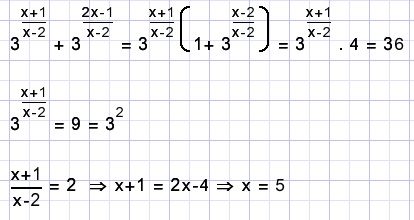
68.
A.
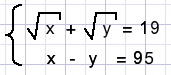
x=? y=?
Solution

B.
x4 + x2 = 90.
x3 = ?
Solution
Let x2 = p.p2 + p - 90 = 0.
(p-9)(p+10) = 0.
p=9.....x=3.....x3 = 27
C.
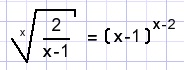
x=?
Solution
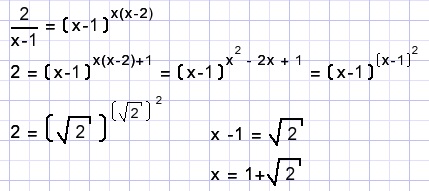
D.
2x = 216
3y = 216
calculate:
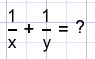
Solution
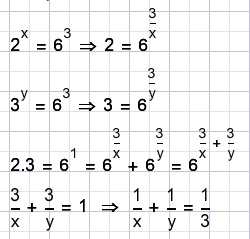
E.
x and y are positive integers.
x2 + 4xy - 12y2 = 148.
Calculate x2 + y2
Solution
148 = 4 * 37148 = 2 * 74
x2 + 4xy - 12y2 = (x + 6y)(x - 2y) = 148.
x + 6y = 37
x - 2y = 4.............no solution in integers
x + 6y = 74
x - 2y = 2...........8y=72..........y=9; x=20
x2+ y2 = 481.
69.
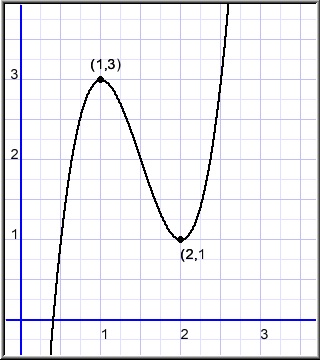
Find the function of above third degree curve.
Solution.
General: y = ax3 + bx2 + cx + d.To find a,b,c,d four equations are needed.
Two result from points (1,3) and (2,1).
These are extremes so, the derivative in these points is zero.
Derivative y'= 3ax2 + 2bx + c.
The four equations are:
a + b + c + d = 3Coefficients a,b,c,d are supplied to the application "LIVE" to solve this system of equations.
8a + 4b + 2c + d = 1
3a + 2b + c = 0
12a + 4b + c = 0

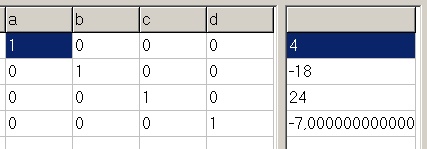
the solution:
Note:
Appliation LIVE may be found [hier].
Solution:
y = 4x3 - 18x2 + 24x - 7

