

 |
Lineaire Functies |  |
 |
Inleiding
 |
| fig.1 |
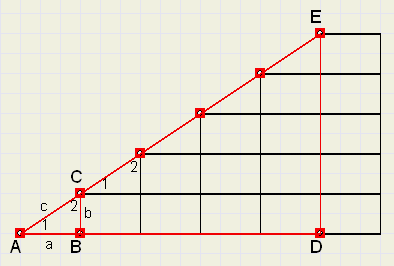
In figuur 1. zien we gestapelde rechthoekjes en twee (rode) driehoeken ABC en ADE.
DADE is een vergroting van DABC met een factor 5.
Als de lengte van AB = a, BC = b en AC = c, dan is AD = 5a, DE = 5b en AE = 5c.
We bekijken de hoeken bij punt C:
-
LC1 + LC2 = 90o , zodat
LACE = 180o
-
AE is een rechte lijn.
met ÚÚn blokje te verhogen.
Stel eens, dat we n horizontale stappen hebben afgelegd, dan zal de stapel op die positie ook n
blokjes hoog zijn.
Als x de horizontaal afgelegde weg is en y de hoogte van de stapel dan zal gelden:
-
x = a.n
y = b.n
| y |
| x |
| b |
| a |
-
y =
| b |
| a |
x kan bijvoorbeeld het aantal liters benzine zijn dat is getankt en y de kosten in euro's.
x heet de onafhankelijke- en y de afhankelijke- variabele.
x is het gegeven waar we van uitgaan, y is het resultaat van een berekening met x.
Een wandeling over de lijn AE kunnen we ons voorstellen als een wandeling over een trap die opgebouwd is
met een enorme hoeveelheid hele kleine blokjes.
Heeft 1 blokje een breedte a en een hoogte b, dan zal op ieder punt van AE gelden: y =
| b |
| a |
de Getallenlijn
 |
| fig.2 |
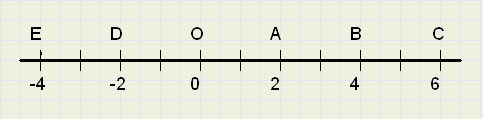
In figuur 2. zie je een getallenlijn afgebeeld.
Een getallenlijn is abstract, want kan van alles voorstellen:
een banksaldo, waterhoogte, kracht, afstand, snelheid, noem maar op.
We hebben aan ÚÚn getal voldoende, om een punt op een getallenlijn aan te geven.
Zo ligt A op positie 2, schrijf A(2) en E op positie -4, schrijf E(-4).
Als we ons op de lijn willen verplaatsen van punt A naar punt C, dan is de volgende
actie nodig : "positie punt C" - "positie punt A" = 6 - 2 = 4, oftewel: afstand 4 naar rechts.
Als we van B naar D willen hetzelfde recept: "aankomst" - "vertrek" = (-2) - 4 = -6 : afstand 6 naar links.
En van E naar C : 6 - (-4) = 10 : afstand 10 naar rechts.
En van C naar B : 4 - 6 = -2 : afstand 2 naar links.
het Rechthoekige Co÷rdinatenstelsel
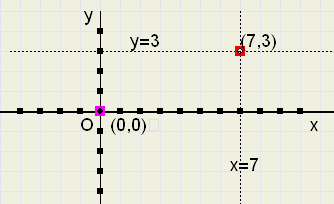
Om de positie van een punt in een plat vlak aan te geven zijn 2 getallen nodig. Zie figuur 3.
 |
| fig.3 |
Er zijn 2 getallenlijnen getrokken:
-
een horizontale, de x-as
een vertikale, de y-as.
Het snijpunt O van de assen wordt de oorsprong genoemd.
Een getal op de x-as of de y-as geeft de afstand aan tot O.
De afspraak is nu, de positie van een punt in het vlak aan te geven met de afstand tot de twee assen.
Eerst x, de horizontale afstand tot de y-as, daarachter y, de vertikale afstand tot de x-as.
Om aan te geven dat de getallen bij elkaar horen worden er haakjes (..) om gezet.
De twee getallen heten de co÷rdinaten van een punt.
Zo heeft de rode punt de co÷rdinaten (7,3).
Die (7,3) zijn op te vatten als een routebeschrijving:
vanuit de oorsprong (0,0) eerst 7 naar rechts en dan 3 omhoog.
In figuur 3 zijn ook twee gestippelde lijnen getekend:
x = 7 : alle punten waarvoor de afstand tot de y-as gelijk is aan 7
y = 3 : alle punten waarvoor de afstand tot de x-as gelijk is aan 3
Het rode punt (7,3) is uiteraard het snijpunt van deze twee lijnen.
Opmerking: voor het punt (-7,-3) is de "route" vanuit de oorsprong:
eerst 7 naar links en dan 3 omlaag.
Het is de gewoonte in het assenstelsel horizontaal aan te geven waar van wordt uitgegaan:
de onafhankelijke variabele.
Vertikaal staat het resultaat van meting of berekening: de afhankelijke variabele.
de Afstand tussen twee punten in een vlak
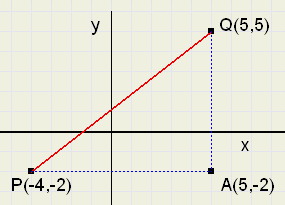
Als de co÷rdinaten bekend zijn, dan is met behulp van de Stelling van Pythagoras de afstand
tussen twee punten te berekenen.
Zie figuur 4.
 |
| fig.4 |
-
PA = 5 - (-4) = 9
QA = 5 - (-2) = 7 zodat
PQ =
| \ | 9 2 + 7 2 |
Algemeen:
De afstand d tussen de punten P(x1,y1) en Q(x2,y2) is
-
d =
| \ | (x2 − x1) 2 + (y2 − y1) 2 |
Recht Evenredig verband
We spreken van een recht evenredig verband tussen de variabelen x en y als geldt:
| y |
| x |
- aantal getankte liters benzine (x) en de prijs (y)
- de uitrekking van een veer (x) en de benodigde kracht (y), binnen bepaalde grenzen uiteraard.
- de hoeveelheid water in een cilindervormige ketel en de waterhoogte
- het aantal maanden sparen (van een constant bedrag) en de grootte van het kapitaal
- tijdsduur en afgelegde afstand, bij constante snelheid.
Voor elke waarde van x kan y worden berekend.
Een getallenpaar x,y kan als punt P(x,y) in een co÷rdinatenstelsel worden getekend.
Indien sprake is van een recht evenredig verband, dan zal elk punt liggen op dezelfde
lijn door de oorsprong. Zie figuur 5.
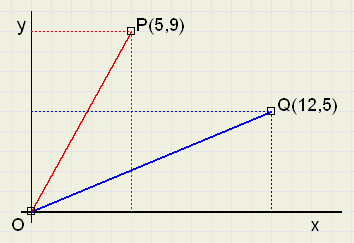 |
| fig.5 |
Beschouwen we eerst de rode lijn:
Op elk punt van de lijn zal gelden
| y |
| x |
| 9 |
| 5 |
of
-
y =
| 9 |
| 5 |
In dit geval is sprake een speciale vergelijking: y staat links in zijn eentje van het "=" teken.
Zo'n vergelijking heet een functie.
Terzijde: de vergelijking x2 + y2 = 100 is geen functie.
In dit artikel gaat het over functies die als grafiek een rechte lijn hebben.
Zulke functies heten lineaire functies.
Lineaire functies komen veel voor in de economie, wetenschap en techniek.
Ook niet lineaire functies (met kromme lijnen als grafiek) kunnen in kleine gebiedjes
als recht worden beschouwd. Denk maar aan het oppervlak van de aarde. Een kaart van de stad
Amsterdam kan zonder bezwaar in een plat vlak worden getekend.
Een rechte lijn trekken van Amsterdam naar Rome zal echter niet lukken.
Terug naar figuur 5:
Voor de blauwe lijn kunnen we de functie opstellen: y =
| 5 |
| 12 |
Voorbeeld 1
De rode lijn heeft als functie y = 1.8x
Neem eens aan, dat y de waterhoogte (meters) is in een vat na x minuten pompen.
Noem de hoogte h en de tijd t, dan gaat de formule over in h = 1,8t.
Wanneer zal de waterhoogte 5,75 meter bedragen?
vul voor h in 5,75 en los op de vergelijking: 5,75 = 1,8t.
Delen door 1,8 levert dan t = 3,194 (minuten).
Voorbeeld 2
We trekken de blauwe lijn door en vragen ons af of het punt S(555,1332) op de lijn ligt.
Welnu, een grafiek wordt gevormd door alle punten waarvoor de vergelijking klopt,
dus invullen maar:
-
1332 = 1,8 * 555 (?) Ja, dat klopt dus S ligt op de lijn.
Ligt punt T(550,988) onder of boven de rode lijn?
Invullen van de waarde van x levert op: y = 1,8*550 = 990.
Het punt (550,990) ligt precies op de lijn, dus (550,988) ligt er net onder.
Voorbeeld 4
Bekijk de metingen in de tabel 1. hieronder:
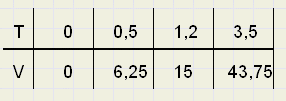 |
| tab.1 |
V is de snelheid in km/uur na T seconden.
We vragen ons af of er tussen V en T een recht evenredig verband bestaat.
In dat geval moet gelden:
| V |
| T |
Dat is zo, want die deling levert steeds 12,5 op.
Voorbeeld 5
Een winkelier koopt twee maal een voorraad van eenzelfde artikel, tegen dezelfde leveringscondities.
De eerste aankoop betreft 50 stuks voor € 640,-
De tweede aankoop betreft 75 stuks voor € 915,-
De vraag is of er sprake is van een recht evenredig verband tussen de prijs en het aantal geleverde
artikelen.
Aankoop 1. : prijs / aantal = 640 / 50 = 12,80
aankoop 2. : prijs / aantal = 915 / 75 = 12,20
De verhouding is niet constant, er is geen recht evenredig verband, omdat er sprake is van
kwantumkorting.
RichtingscoŰfficiŰnt
Bekijk nog eens figuur 5.
De rode lijn loopt steiler omhoog dan de blauwe.
Dat komt omdat bij de rode lijn de verhouding
| y |
| x |
Noemen we deze verhouding a (een andere a dan in figuur 1 dus), dan is y = a.x.
-
y = a.x is de algemene formule van een recht evenredig verband.
bekijk het ook zo: steeds als x 1 toeneemt, neemt y toe met waarde a.
Hoe groter a, hoe steiler de grafiek omhoog loopt.
De x-as is op te vatten als de grafiek van de functie y = 0
De y-as kan alleen worden geschreven als x = 0 omdat er geen richtingscoŰfficiŰnt bestaat
voor recht omhoog lopende lijnen (of die moet oneindig groot zijn, maar daar is niet mee
te rekenen).
In sommige leerboekjes wordt het woord "hellingsgetal" gebruikt in plaats van richtingscoŰfficiŰnt.
Dat laatste woord korten we voortaan af met rc.
Een rechte lijn ligt vast als er 2 punten van bekend zijn.
De grafiek van een recht evenredig verband gaat altijd door de oorsprong.
Is buiten deze oorsprong nog een punt bekend, dan kan de formule erbij worden berekend.
Loodrecht
Bekijk figuur 7 hieronder.
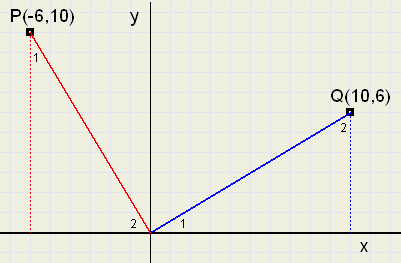 |
| fig.7 |
De rode en blauwe driehoeken zijn gelijk en de hoeken gemerkt 1.. en ..2 zijn samen 90 graden.
Daarom staan de lijnen OP en OQ loodrecht op elkaar.
Voor de blauwe lijn geldt: rc a1 =
| 6 |
| 10 |
Voor de rode lijn geldt : rc a2 =
| 10 |
| −6 |
| 10 |
| 6 |
Opmerking: een negatieve rc. zorgt voor een daling van y bij toename van x.
We zien hier een recept om de rc. van een lijn te vinden, die loodrecht op een bekende lijn staat:
verwissel teller en noemer en vermenigvuldig met (-1).
Algemeen:
-
als de grafieken van y = a1x en y = a2x loodrecht op elkaar staan dan is
a2 = −
| 1 |
| a1 |
We kunnen ook schrijven: a1.a2 = -1
Een willekeurige rechte lijn
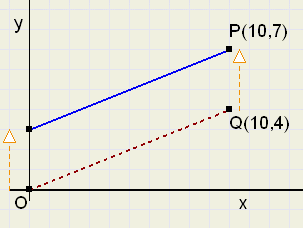 |
| fig.8 |
De formule bij de gestippelde lijn is y = 0,4x
De blauwe lijn is de evenwijdige verschuiving hiervan met 3 omhoog, zodat y = 0,4x + 3.
Algemeen:
-
een rechte lijn met rc = a, die de y-as snijdt in het punt b heeft als functie y = ax + b
Een lijn met rc = 2 snijdt de y-as in het punt (0,10).
Alle lijnen : y = ax + b.
Als a = 2 en b = 10, dan wordt de formule: y = 2x + 10.
Voorbeeld 7
Een lijn met rc = 2 snijdt de x-as in het punt (10,0).
Alle lijnen : y = ax + b.
Als a = 2 dan y = 2x + b , dat zijn alle lijnen met rc = 2
Punt (10,0) ligt op de lijn dus moet gelden: 0 = 2*10 + b, dus b = -20,
(10 invullen voor x, 0 invullen voor y)
de formule wordt: y = 2x - 20.
Voorbeeld 8
Een lijn gaat door het punt (8,15) en loopt evenwijdig aan y = 0,5x
Alle lijnen : y = ax + b.
Lijnen evenwijdig betekent: gelijke rc's, dus y = 0,5x + b.
Punt (8,15) op de lijn, dus invullen maar: 15 = 0,5*8 + b en b = 11.
De formule luidt: y = 0,5x + 11.
Voorbeeld 9
Een lijn gaat door het punt (8,15) en staat loodrecht op de lijn y = 0,5x
Alle lijnen : y = ax + b.
Loodrecht, dus a.0,5 = -1 dus a = -2, dat wordt y = -2x + b.
Punt (8,15) op de lijn, dus invullen maar: 15 = -2*8 + b en b = 31.
De formule luidt: y = -2x + 31.
Stel dat een lijn de x-as snijdt in het punt (c,0).
Algemeen: y = ax + b. We proberen de b door c te vervangen.
(c,0) op de lijn, dus invullen: 0 = a.c + b, zodat b = -a.c en de formule
wordt: y = ax -ac of y = a(x - c).
-
y = a(x - c) is de algemene formule voor een lijn met rc = a,
die de x-as snijdt in punt c.
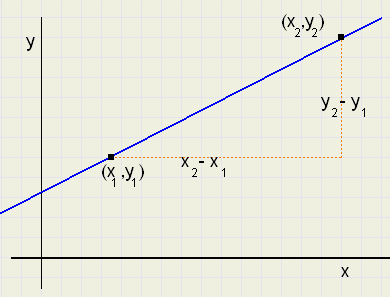 |
| fig.9 |
algemeen: y = ax + b.
In fig. 9 is de rc. a =
| y2 − y1 |
| x2 − x1 |
en omdat (x1,y1) op de lijn ligt: y1 = ax1 + b
zodat b = y1 - ax1
Overzichtelijker:
-
y = a(x - x1) + y1
is de algemene formule voor een rechte lijn door de punten (x1,y1) en (x2,y2),
waarbij
a =
| y2 − y1 |
| x2 − x1 |
Anders bekeken: stel je een willekeurig punt P(x,y) in het vlak voor.
Onder welke voorwaarden van x en y zal P dan op de lijn liggen?
Welnu, we stellen ons op in het eerste punt (x1,y1) en kijken langs het tweede punt naar P.
Ligt P in het verlengde van het tweede punt, dus bij gelijke rc's van P naar elk punt, dan
zal P op de lijn liggen.
Maar dan geldt (gelijke rc's):
| y − y1 |
| x − x1 |
| y2 − y1 |
| x2 − x1 |
of:
y − y1 = a (x − x1)
Voorbeeld 10
Gevraagd de lijn door (-6,4) en (12,25) en de snijpunten met de assen.
-
a =
| 25 − 4 |
| 12 − −6 |
| 7 |
| 6 |
y − 4 =
| 7 |
| 6 |
y =
| 7 |
| 6 |
y =
| 7 |
| 6 |
De vergelijking moet kloppen.
Het snijpunt met de y-as is direct te noemen: (0,11).
Om het snijpunt met de x-as te vinden vullen we voor y 0 in: 0 =
| 7 |
| 6 |
zodat x = −
| 66 |
| 7 |
Afstand tussen parallelle lijnen
In figuur 10 zie je de twee parallelle lijnen:
-
y = ax
y = ax + b
-
OB = b
AB ^OD
AB = d, de te berekenen afstand
OC = 1 , zodat CD = a
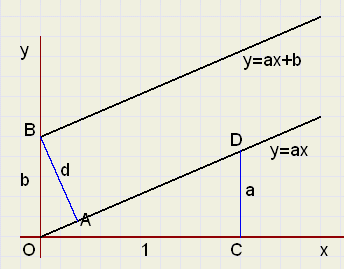 |
| fig.10 |
Pythagoras:
-
O D =
| \ | a 2 + 1 |
-
d : b = 1 : OD
d =
| b |
| O D |
| d | = |
|
-
y = ax + b1
y = ax + b2
-
b = b1 - b2
| d | = |
|
Lijn 1 snijdt de y-as in (0,20)
Lijn 2 snijdt de y-as in (0,15) en loopt parallel aan lijn 1.
Bij welke rc. is de afstand tussen de lijnen precies 1?
| d | = |
|
| 1 | = |
|
| \ | 24 |
Snijpunt van twee lijnen
We gaan uit van de lijnen
-
y = 2x - 5
y = 0,5x + 7
zodat
2x - 5 = 0,5x + 7
1,5x = 12
x = 8
invullen in eerste vergelijking:
y = 2.8 - 5 = 11
het snijpunt is (8,11).
Met een lineair verband wordt bedoeld, dat de grafiek een rechte lijn is.
Het recht evenredige verband is dus een speciaal geval van een lineair verband
(de lijn gaat door de oorsprong).
Of er tussen metingen een lineair verband bestaat kan als volgt worden aangetoond:
Teken punten, ga uit van 1 punt en bereken de rc. van alle lijnen naar de andere punten.
Deze rc.'s moeten gelijk zijn bij een lineair verband.
Voorbeeld 12
Ga na of er een lineair verband bestaat en zo ja, welk:
| meting | 1 | 2 | 3 |
| x = | 4 | 8 | 36 |
| y = | -13 | -11 | 3 |
| tab. 2 | |||
| −11 − −13 |
| 8 − 4 |
Vergelijk meting 1 en 3:.....rc =
| 3 − −13 |
| 36 − 4 |
Er is dus een lineair verband.
y = 0,5x + b
Punt (4,-13) invullen:....-13 = 0,5.4 + b
b = -15 en de formule luidt:.....y = 0,5x - 15
Voorbeeld 13
Een punt P ligt op afstand 10 van het punt Q(100,15) en de lijn y = 0,2x - 5.
(PQ staat loodrecht op de lijn)
Gevraagd, de co÷rdinaten van P.
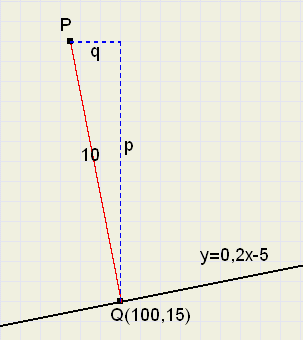 |
| fig.11 |
ook is : p2 + q2= 10, dus
25q2 + q2 = 102
26q2 = 100
q = 1,96 en p = 5q = 9,8.
Voor de co÷rdinaten van P geldt dus:
x = 100 - q = 100 - 1,96 = 98,04 en
y = 15 + p = 15 + 9,8 = 24,8
Een toepassing
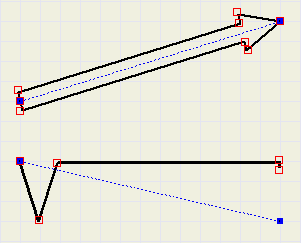 |
| fig.12 |
Een ontwerper wil op een beeldscherm een wortelteken en een pijl afbeelden.
De grootte is afhankelijk van de afgelegde afstand van de muis.
Windows levert per muisbeweging de co÷rdinaten (x,y) van de muispijl.
In figuur 12. zijn de muisbewegingen blauw aangegeven.
Bij het eerste punt werd de muisknop ingedrukt, bij het tweede punt werd de muisknop
losgelaten.
Uit de begin- en eindco÷rdinaten worden de co÷rdinaten van de rode punten berekend.
Hiervoor is de theorie hierboven toereikend.
De pijl en het wortelteken ontstaan door tussen de rode punten lijnen te tekenen.
Programmeertalen bevatten al procedures voor het tekenen van lijnen.
Als dat niet het geval is, dan moet de formule bij elke lijn worden berekend en moet
elk punt van de lijn afzonderlijk worden ingekleurd.
Dat is ook nodig als bijvoorbeeld de kleur van een lijn zou moeten verlopen.


