Staatsexamen meetkunde, kweekschool (1957)

Vooraf

Regelmatig wordt in de media bericht over de geringe rekenkundige vaardigheden van de PABO studenten.
Hoe was dat vroeger?
Daarom hieronder het Onderwijzers-Staatsexamen vlakke meetkunde en goniometrie van 1957.

De antwoorden en uitwerkingen zijn van mijzelf.

Opgave 1

Van een trapezium ABCD zijn de evenwijdige zijden AB en CD.
Door het snijpunt S van de diagonalen trekt men een lijn evenwijdig aan AB, die AD snijdt in P en BC in Q.
AB = 50, BC = 26, CD = 22 en AD = 30 (cm).

a. bereken de afstand van de evenwijdige zijden

Zie de figuur hieronder: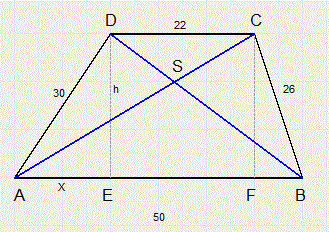
AE = x, DE = CF = h
Pythagoras in DAED en DBFC
    h2 = AD2 - x2
    h2 = BC2 - (AB - x - CD)2

    302 - x2 = 262 - (50 - x - 22)2
    x = 18
    h = 24

b.bereken de lengte van diagonaal BD

    BE = 50 - 18 = 32
    BD2 = 322 + 242 = 1600
    BD = 40

c.bewijs, dat LADB = 900

    AD2 + BD2 = 302 + 402 = 2500 = AB2
Omgekeerde stelling van Pythagoras.

d.bereken de lengte van PQ

Zie figuur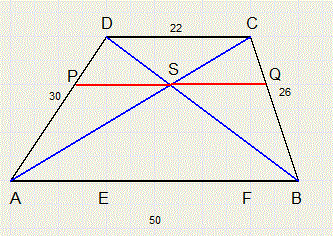
Bij deze opgave bekruipt mij wat twijfel.
Het leerboekje ( Planimetrie Goniometrie en Trigonometrie voor de Kweekschool, Noordhoff 1961)
bevat overeenkomstige opgaven en ook wat stellingen over trapeziums.
De vraag is in hoeverre de leerlingen van deze resultaten gebruik mochten maken.

Laten we dat eens niet doen en ons behelpen met gelijkvormigheid van driehoeken.
    D SPA ~ D CDA
    dus:
    PS : CD = AP : AD

    D PSD ~ D ABD
    dus:
    PS : AB = DP : AD

    Stel eens, dat DP : PA = x : y
    En ook, AB = a, CD = c
    dan zien we :
    ax = cy oftewel x : y = c : a

    Voor PS geldt dan:
    PS : a = x : (x+y)
    PS = ax /(x+y) = ac/(a+c)...........{deel teller en noemer door y}
    Met gelijkvormigheid is ook te zien dat PS = SQ
    Dus PQ = 2ac/(a + c)
    PQ = 2.50.22/(50 + 22) = 30 5/9

e.hoe groot is de cosinus van LDAB?

    cos LDAB = BD / AB = 4/5

Opgave 2

Construeer een regelmatige zeshoek ABCDEF met een zijde van 4 cm. en trek hierin
de diagonalen AC,BD,CE, DF,EA,FB.

Een regelmatige zeshoek is opgebouwd uit gelijkzijdige driehoeken.
We construeren eerst zo'n driehoek en roteren die steeds 600 om de tophoek
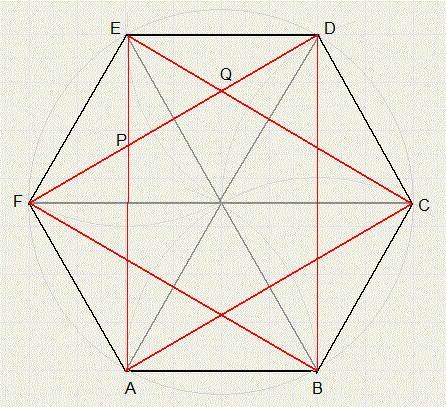
(4 cm. omgecirkeld vanuit B levert C, vanuit C levert D, enzovoorts)

a.bewijs dat deze diagonalen gelijk zijn en elkaar in drie gelijke stukken verdelen

De diagonalen zijn gelijk wegens rotatiesymmetrie om het middelpunt.

Met de stelling van Thales is meteen uit de figuur de grootte van een hoek af te lezen.
Zo is LEFD = 300 want staat op een cirkelboog van 360/6 = 600

Zodoende is PQE een gelijkzijdige driehoek (alle hoeken zijn 600)
Driehoeken FPE en EQD zijn congruent en gelijkbenig.
Daarom is FP (=PE) = PQ (=QE) = QD

b.bereken de lengte van de zijde van de regelmatige zeshoek,
die door de getrokken diagonalen wordt gevormd

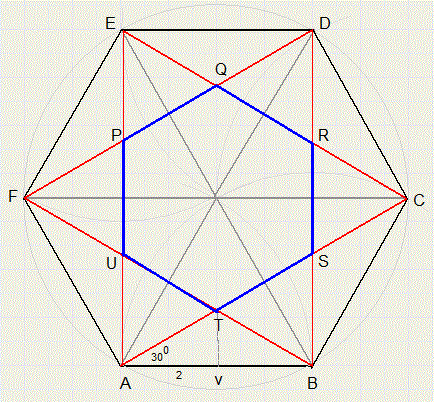
    TV : AT = 1 : 2 ....{helft van gelijkzijdige driehoek}
    Stel TV = x, dan AT = 2x
    4 + x2 = 4x2
    3x2 = 4
    AT = TU =
    4
    3
     
    \3

c.bewijs dat de oppervlakte van deze zeshoek het derde deel is van de oppervlakte
van de oorspronkelijke zeshoek

De oppervlakten verhouden zich als de kwadraten van hun zijden, immers gelijkvormige figuren.
TU2 : AB2 = 1 : 3

Naschrift

De meetkunde is van redelijk niveau al is onduidelijk welke formules de leerlingen paraat hadden.
De goniometrie komt niet aan bod, terwijl het leerboekje een redelijk niveau heeft.
Maar dit was ook maar deel 1 van het Staatsexamen.