speciale kwadraten

Speciale kwadraten

download programma

download Delphi project

Ik vroeg mij af of er kwadraten bestaan van 10 cijfers die elk cijfer 0..9 bevatten.
Het kleinst mogelijke kwadraat is dan 0123456789 maar de wortel daarvan is 11111.xxxxx , geen geheel getal.
Het grootste getal zou zijn 9876543210 wat het kwadraat is van 99380.xxxx , ook geen geheel getal.

Daarom een programma geschreven.
Er zijn twee benaderingen:
1.
maak alle permutaties van de elementen 0..9, dat zijn er 10!=3628800.
Bereken de wortel van elk en test of dit een geheel getal is.
2.
Tel van 11111 tot 99380, kwadrateer elk getal en test of het alle cijfers 0..9 bevat.
Methode 2 is gekozen.

Mijn Delphi versie is 32 bit dus het getal 9876543210 past niet helemaal want
het bereik van het type cardinal is 0..4294967295.
Dit is te ondervangen door het getal over 16 bit words te verdelen.
Bij 4 cijfers per word rekenen we in feite in het 10000 tallig stelsel (0000..9999).
Deze methode (2A) beschrijf ik eerst.

Delphi-7 ondersteunt beperkt 64 bit integer (Int64) bewerkingen en ook de inttostr functie doet dat.
Het gebruik hiervan, methode (2B) beschrijf ik daarna.

Methode 2A
num is het getal waar we mee beginnen.
De beginwaarde is 11111.

Stappen:
1 - kwadrateer num, dat kwadraat is num2.
2 - test of num2 de cijfers 0..9 bevat.
3 - zo ja, voeg num en num2 toe aan een Tmemo component.
4 - verhoog num.
herhaal stappen 1..4 tot num de waarde 99380 bereikt.

Data formaten

var num   : array[0..1] of word;
    num2  : array[0..2] of cardinal;//square of num
    snum2 : string;                 //string of num2

num: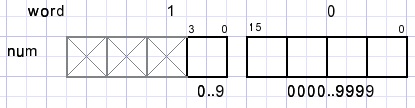

num2:

Procedures

procedure incNum;
//increment num
begin
 inc(num[0]);
 if num[0] = 10000 then begin
                          num[0] := 0;
                          inc(num[1]);
                        end;
end;

procedure squareNum;
//make num2
var i,j : byte;
begin
 for i := 0 to 2 do num2[i] := 0; //clear
 for i := 0 to 1 do
  for j := 0 to 1 do
   begin
    num2[i+j] := num2[i+j] + num[i]*num[j];
   end;
 for i := 0 to 2 do
  if num2[i] > 10000 then
   begin
    num2[i+1] := num2[i+1] + (num2[i] div 10000);
    num2[i] := num2[i] mod 10000;
   end;
end;

function test : boolean;
//test num2 for digits 0..9
var dbits,w: word;
    d,i : byte;
begin
 w := 0;
 dbits := 0;
 snum2 := '';
 for i := 0 to 9 do
  begin
   case i of
    0 : w := num2[0];
    4 : w := num2[1];
    8 : w := num2[2];
   end;
   d := w mod 10;
   w := w div 10;
   dbits := dbits or (1 shl d);
   insert(chr(ord('0')+d),snum2,1);
  end;//for
 result := dbits = $3ff;
end;

procedure TForm1.Button1Click(Sender: TObject);
//GO
begin
 memo1.Clear;
 num[0] := 1111;
 num[1] := 1;
 repeat
  squareNum;
  if test then report;
  incNum;
 until (num[1] = 9) and (num[0] > 9380);
 label1.Caption := 'squares found: '+inttostr(memo1.Lines.count);
end;

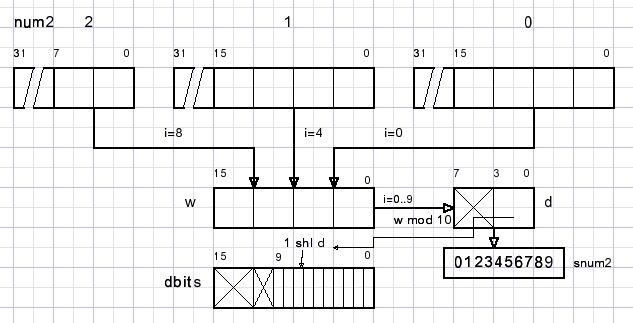
Unieke cijfer test
Pak de 10 cijfers uit num2.
Set bit d in word dbits voor cijfer d.
Na geslaagde test heeft variable dbits de waarde $3ff.

Methode 2B
Met gebruik van 64 bit integers (Int64).

procedure TForm1.Button2Click(Sender: TObject);
//GO-2B
var t1,t2,n,n2 : Int64;
    w : word;
    s,sn : string;
    d,i : byte;
    pt : double;
begin
 memo1.Clear;
 n :=11111;
 t1 := GetCPUticks;
 repeat
  n2 := n*n;
  sn := inttostr(n2);
  if length(sn) = 9 then insert('0',sn,1);
  w := 0;
  for i := 1 to 10 do
   begin
    d := byte(sn[i])-ord('0');
    w := w or (1 shl d);
   end;
  if w = $3ff then memo1.Lines.Add(inttostr(n)+'  '+sn);
  inc(n);
 until n > 99380;
 t2 := GetCPUticks;
 s := 'squares found: '+inttostr(memo1.Lines.count);
 pt := 0.001*proctime(t2-t1);
 s := s + '; time= '+formatfloat('###0.000',pt)+ ' msecs';
 label1.Caption := s;
end;

Rekentijden
Door even de memo1.lines.add( ) statements te onderdrukken meten we preciese rekentijden.
Methode 2B blijkt dan zo'n 10 keer sneller te zijn als methode 2A.

CPU clock
Functie GetCPUticks levert het aantal CPU clock cycles sinds power on.
Procedure setCPUclock zet variable clockrate op de juiste waarde bij het starten van het programma.
Functie proctime geeft de verstreken tijd in micoseconden.
Zie de timer unit code.

Hiermee besluit ik deze beschrijving.