kleuren compressie

Een onderzoek naar betere kleuren compressie

	download demonstratie programma
	download Delphi-7 project

Wanneer we onderzoek plegen is het natuurlijk prettig om resultaten te behalen die aan de verwachtingen voldoen.
Is nu ons onderzoek als mislukt te beschouwen als die resultaten tegenvallen?
Ik denk het niet.
Immers, onderzoek vindt juist plaats omdat de resultaten niet vaststaan.
Ook onderzoek dat aantoont dat iets niet kan is waardevol omdat het wel degelijk de kennis verhoogt.
Daarom publiceer ik hier een onderzoekje dat niets heeft opgeleverd.

Voordat u dit artikel wegklikt noem ik nog dat er methodes worden uitgelegd om

In een eerdere publicatie heb ik bericht van een project (SPIC) voor de compressie van images.
Eén van de stappen was de reductie van een 24bit- naar 12 bit kleurcode.
Per kleur (r,g,b) zijn er dan nog maar 4 bits, wat 16 tinten mogelijk maakt.
Dat levert voor de meeste foto's voldoende kwaliteit,
maar bij de lichtere kleuren zoals wolkenluchten trad wat verkleuring op.

Het idee is dit: het oog lijkt meer gevoelig voor lichte dan donkere kleuren.
Maak daarom een conversie tabel van kleurcode (0..15) naar kleurintensiteit die
een fijnere instelling van lichte kleuren geeft, ten koste van een wat grovere instelling van de donkerder tinten.

Eerst het afronden van kleuren zoals toegepast in het oude SPIC project:
Een 24 bits kleur heeft 8 bits r,g,b velden.
De conversietabel van kleurcode naar 8 bits kleur is

code	8 bit kleur
0	$0f
1	$1f
....	....
$f	$ff

De conversie van 8 bits kleur K naar code X gaat zo:

$ff levert dus kleurcode $f, $f7 levert kleurcode $e.

We wensen voor de lichtere kleuren kleinere stappen tussen opvolgende kleurcodes.
Kleuren $f8 .. $ff leveren nu code $f.
Laten we daarvan maken: $fc .. $ff geeft code $f , $f8 .. $fb geeft code $e

Echte kleuren $f8, $f9, $fa, $fb geven code $e
Echte kleuren $fc, $fd, $fe, $ff geven code $f.

Het omslagpunt tussen codes $e en $f ligt dus bij kleur $fc.

Om de andere omslagpunten te vinden kiezen we voor een kwadratische functie

waarbij X de 4 bits code is en K de 8 bits kleur.

De variabelen A,B,C kunnen we uitrekenen als we uitgaan van 3 paren (K,x)
Onderstaande tabel geeft de 3 keuzes weer

code X	8 bit kleur K
X1 : 0	K1 : 0
X2 : 10 ($a)	K2 : 198 ($c6)
X3 : 15 ($f)	K3 : 252 ($fc)

Om te experimenteren moeten we K en X kunnen kiezen, dus eerst lossen we algemeen
het volgende stelseltje lineaire vergelijkingen op:

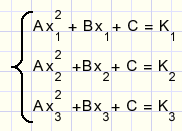
C is te elimineren door het verschil tussen 2 regels te nemen (regel1-regel2,regel2-regel3):

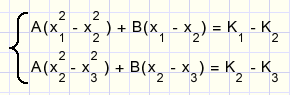
Om schrijfwerk te besparen stellen we:

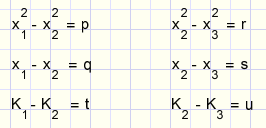
Wat het stelsel oplevert:

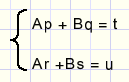
vermenigvuldigen (*s regel 1, *q regel 2) :

verschil nemen, delen en invullen in vorige vergelijkingen:

Hieronder is de de functie geplot

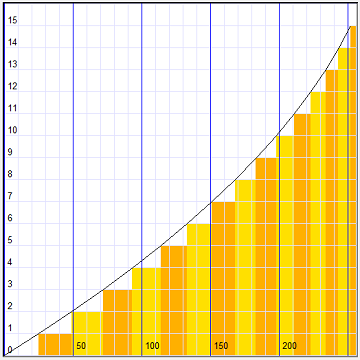
Vertikaal de kleurcodes X , horizontaal de kleur K waarvoor de code wijzigt.
We zien dat voor de lichtere kleuren de kleurwaardes dichter bij elkaar liggen.
Hierboven zien we de omslagpunten, maar de echte kleurwaardes liggen (afgerond)
tussen twee opvolgende omslagpunten in, dus halverwege de geel/oranje kolommen.

Uitgaande van een kleurcode X is de (omslag) kleur K te vinden door X
in de formule in te vullen en K uit te rekenen.

Maar hoe vinden we de kleurcode X uitgaande van een 8 bits kleur K?
Dat kan met de ABC formule om kwadratische vergelijkingen op te lossen,
de analytische manier. Maar er is ook een numerieke methode.
Om die te demonstreren eerst een simpel voorbeeld: we moeten een getal < 16 raden.
Dat doen we door een vraag te stellen zoals: “is het getal groter dan......”.
Per antwoord (1 bit informatie) halveert het aantal keuzes en na 4 keer raden hebben we dan het getal te pakken.

Twee variabelen doen het werk : Base en Step.
K is het te raden getal onder de 16.
Zie de flowchart :

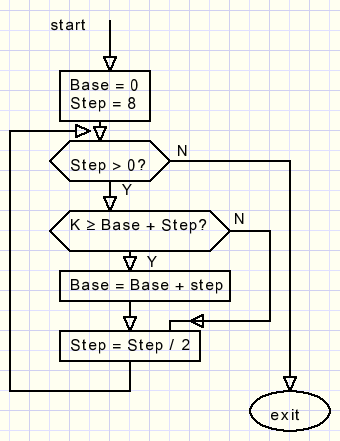
Step halveert na elke vraag. Na 4 vragen is Step nul geworden en Base is het antwoord.
Voor ons probleem is moet alleen de vraag K >= Base + Step vervangen worden door

K>= tabel[Base + Step] ? Da's alles.

Hieronder wat programma codes.
Eerst het berekenen van de coëfficiënten A,B,C.

procedure makeABC;
var p,q,r,s,t,u : double;
begin
 p := sqr(x1)-sqr(x2);
 q := x1-x2;
 r := sqr(x2)-sqr(x3);
 s := x2-x3;
 t := y1-y2;
 u := y2-y3;
 A := (t*s - u*q)/(p*s - r*q);
 B := (t- A*p)/q;
 C := y1 - A*sqr(x1) - B*x1;
end;

De 3 getallen paren (code,kleur) zijn: (x1,y1) (x2,y2) en (x3,y3).
Dus x is de code, y de (omslag) kleur.
X en Y komen uit Tedit components.

Dan maken we een tabel voor de omslagwaarden (basevalues) en ook een voor de echte
kleurwaarden (penvalues): (i is de code)

procedure makebasevalues;
var i : byte;
begin
 for i := 1 to 15 do baseValue[i] := trunc(a*sqr(i) + B*i + C);
 baseValue[0] := 0;
end;

procedure makePenValues;
var i : byte;
begin
 for i:=0 to 14 do 
   penValue[i]:=(baseValue[i]+baseValue[i+1]+3) shr 1;
 penvalue[15] := $ff;
end;

En de functie om de code te vinden uit de kleur: ( x is de kleur, result is de code)

function findIndex(x : byte) : byte;
//find closest index in basevalue array for x
var base,range : byte;
begin
 base := 0;
 step := 8;
 repeat
   if x >= basevalue[base+step] then base := base + step;
   step := step shr 1;
 until step = 0;
 result := base; 
end;

Het Delphi-7 project heeft 3 bitmaps:

Ook zijn er 3 paintboxen om deze bitmaps af te beelden.

Hieronder een verkleinde afbeelding van het project in werking, links het origineel, rechts nadat de slimme kleurcompressie heeft plaatsgehad.
Het plaatje toont het Verenigd Koninkrijk dat net op tijd ontsnapt aan de ondergang van de EU.

Dit artikel begon ik met de mededeling dat al dat gereken weinig heeft opgeleverd.
Om dat te zien kan beter een demo image worden bekeken.
Hieronder de resultaten : links het origineel in 8 bits kleuren,
midden de simpele afronding en rechts de slimme afronding op 4 bits kleuren

Bij de rechter afbeelding is duidelijk te zien dat de donkerder kleuren in grovere stappen verlopen.
De winst bij de lichtere kleuren valt nauwelijks op.

Voor meer details verwijs ik naar de source code.