Het kikkersprongen spel

Inleiding

Op het web trof ik de "leap-frog puzzle" aan, een puzzeltje voor kinderen.
Klik [hier] om het te spelen.
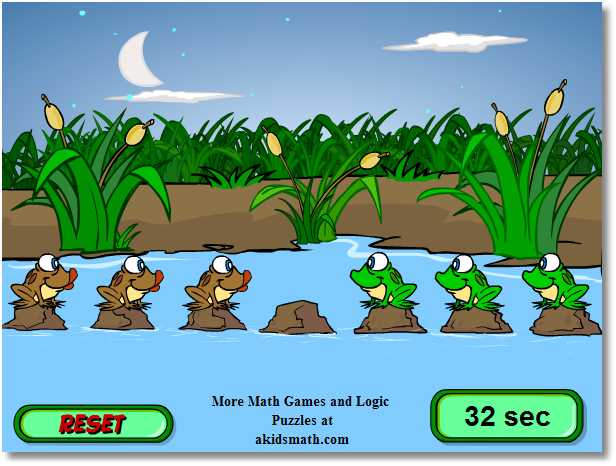
Het bestaat uit 2 groepjes van 3 kikkers tegenover elkaar, met 1 open plaats tussen hen in.
De bedoeling is de kikkers zodanig te laten springen, dat ze van plaats verwisselen.
Daarbij mag een kikker alleen naar voren springen naar een open plaats ernaast of over één andere kikker.

Om nog wat origineels toe te voegen heb ik de kikkers door berggeiten vervangen en het spel
"bokkesprongen" genoemd.
Ook heb ik een paar niveaus ingevoerd.
Klik [ hier] om "bokkesprongen" te spelen.

In dit artikel leg ik uit hoe met een (Delphi) computerprogramma dit puzzeltje oplost.
Tevens wordt een formule afgeleid voor het aantal benodigde sprongen als er 2 groepjes van k kikkers
tegenover elkaar staan.
Er is geen moeite gedaan om mooie springende kikkers of bokken te tekenen.
In plaats daarvan noem ik de 3 linker kikkers X en de 3 rechter kikkers Y.

Dit is dan de beginstand van de puzzle:
Springen doen de kikkers als volgt:
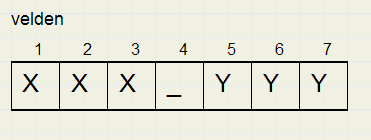
    - een X kikker springt alleen naar rechts
    - een Y kikker springt alleen naar links
    - een kikker springt naar een open plaats direct ernaast of
    - over 1 kikker ernaast naar een open plaats
De puzzle is opgelost als de eindstand Y Y Y - X X X is bereikt.

Codering

De plaats waar een letter staat noem ik een "veld".
Een veld bevat : geen kikker, een X- of een Y kikker.

type TkikkerSoort = (geen,  kX, kY)
var speelveld : array[1..6] of TkikkerSoort;
Hoewel een sprong met het veldnummer kan worden aangegeven is het handiger
om ook het veld waar de kikker heen springt te onthouden.
type Tsprong = record
                org , dest : byte; //begin- en eindveld van een kikkersprong
               end;

var sprongen : array[1..20] of TSprong;  //alle gemaakte sprongen
    sprongNr : byte = 0;  // de laatste sprong
Hieraan hebben we voldoende om aan de slag te gaan.

Procedures en Functies

In het programma kan, met KikkersUpDown control, het aantal kikkers per soort worden ingesteld van 1 tot en met 10.
Het aantal kikkers wordt met k aangegeven.
Het aantal velden is dan w = 2 * k + 1

procedure kikkersOpstellen zet de velden van array speelveld op de beginstand.
Voor het tekenen van een veld wordt procedure TekenVeld aangeroepen.

functie zoekoplossing levert resultaat "true" af als een oplossing is gevonden.
Deze functie is karakteristiek voor het zoeken van oplossingen volgens de "brute kracht" methode.
Daarbij worden systematisch alle mogelijkheden op het speelveld doorlopen.
Hieronder de flowchart:
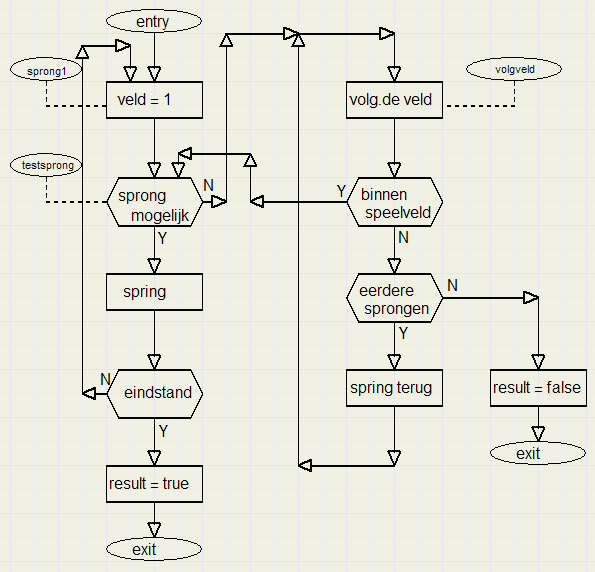
"veld" heet in de source listing "van" , het veld waar-van-daan wordt gesprongen.
Omdat er een paar programma-lussen door elkaar heen lopen is gestructureerd programmeren niet handig.
Een paar labels en goto statements zijn hier, bij uitzondering, duidelijker.

De functie sprongOK(nr : byte) : byte onderzoekt of de kikker in veld nr kan springen.
Als dat zo is dan levert de functie het veld waarnaar dan gesprongen kan worden, anders is het resultaat 0.

Hier kan men makkelijk verzanden in een woud van if...else statements, die erg onoverzichtelijk worden.
Handiger is de situatie te coderen en de code aan een case statement aan te bieden.

Het werkt als volgt:
Zet code = $10 voor een X kikker en code = $20 voor een Y kikker.
Zoek daarna alle velden af om de lege plaats te vinden.
Verander de code afhankelijk van de positie van die lege plaats :
1 voor 1 rechts, 2 voor 2 rechts, 4 voor 1 links en 8 voor 2 links.
Zodat nu bij de volgende codes deze resultaten horen
    - $11....... 1 rechts
    - $12....... 2 rechts
    - $14....... 1 links
    - $18....... 2 links

De Knoppen

We willen natuurlijk de gevonden oplossingen naspelen.
Ook is het wel aardig om zelf naar oplossingen te zoeken.
Daarom zijn er 3 speedbuttons geplaatst:

playBtn

Om zelf oplossingen te zoeken. Plaats de muispointer op de X of Y en klik om te zetten.

analyseBtn

Om de computer naar oplossingen te laten zoeken.

replayBtn

Om een oplossingen stap voor stap te tonen.

Nog 2 bitbuttons zijn toegevoegd:

goBtn

Het opschrift wordt steeds aangepast aan de ingedrukte speedbutton.
De knop zorgt voor terugspringen (bij playBtn.down), starten van zoekproces (analyseBtn.down) of
het tonen van de volgende sprong (replayBtn.down).

clearBtn

Met deze knop wordt het speelveld in de beginstand gezet.

Voor verdere details verwijs ik naar de source listing.
Die kan je [ hier ] downloaden.
Klik op het bliksem icoon bovenaan de pagina om alleen het programma te downloaden.

Wiskunde

Als er k kikkers van elke soort zijn dan heeft het spel w = 2k + 1 velden.
Elke kikker moet tot de eindstand k + 1 velden verspringen, dus totaal moeten er 2k(k + 1)
velden worden versprongen.
Elke kikker moet bovendien minimaal over 3 andere kikkers heen springen,
dat zijn k*k sprongen van 2 velden, waarbij dus 2k*k velden worden afgelegd.
Er vinden dus maximaal 2k(k + 1) - 2*k*k = 2k enkelvelds sprongen plaats.
Maximaal aantal sprongen is dus k*k + 2k = k(k + 2).

Een spel met 3 kikkers per soort wordt dus maximaal in 3 * 5 = 15 zetten opgelost,
waarbij we nog niet hebben bewezen dat die oplossing ook bestaat.

Het programma toont echter aan dat er steeds 1 oplossing is in k(k + 2) zetten.