de hoogte van een berg

de Hoogte van een Berg

In dit artikel bedenken we een formule om uit twee metingen de hoogte van een berg te berekenen.
De benodigde voorkennis is eenvoudige goniometrie en het oplossen van twee vergelijkingen met
twee onbekenden.

Bekijk het plaatje hieronder:

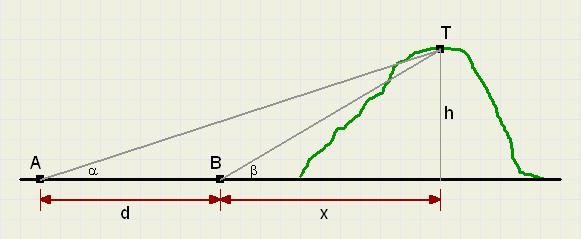Vanaf punt A wordt de hoek (a) gemeten waaronder de top T wordt gezien.
Voor de tweede meting verplaatsen we ons over een afstand d naar punt B en meten opnieuw de hoek (b).

Nu is het volgende bekend:

tan a =

d + x

tan b =

Uit deze twee vergelijkingen verwijderen we x, waarna een formule van de vorm h = ...... overblijft.

Uit de eerste formule volgt:

h = (d + x) · tan a

Uit de tweede formule volgt:

h = x · tan b

Dit combinerend:

(d + x) · tan a = x · tan b

d · tan a + x · tan a = x · tan b

d · tan a = x · tan b − x · tan a

d · tan a = x ( tan b − tan a)

x =

d · tan a

tan b − tan a

Deze formule van x substitueren we in h = x · tan b
zodat:

h =

d · tan a · tan b

tan b − tan a