

 |
de Som van de Hoeken van een Driehoek |  |
 |
Inleiding
Zoals je in het voortgezet onderwijs na een paar lessen wiskunde weet,
is de som van de hoeken van een driehoek 180 graden.
Dit artikel geeft een drietal bewijzen van deze eigenschap.
In de vlakke meetkunde werken we met rechte lijnen, hoeken en cirkels.
Een rechte lijn is de kortste verbinding tussen twee punten.
Denk daarbij aan een strakgespannen touwtje.
Hoeken ontstaan als twee lijnen elkaar snijden.
De hoek tussen lijnen geeft het verschil in richting aan tussen die lijnen.
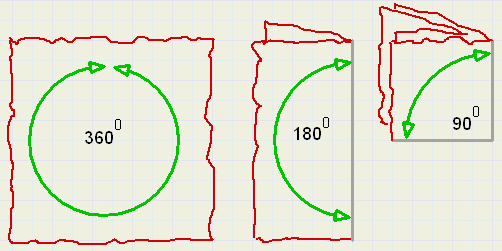
Afspraak is, dat bij een gehele ronde een hoek hoort van 360 graden.
Voor wat betreft de richting, is 360 graden gelijk aan 0 graden.
Een rechte lijn is op te vatten als een hoek van 180 graden.
Vouwen we een blad papier doormidden, dan komt dat neer op delen van een hoek van 360 graden
in twee hoeken van 180 graden.
Bij nogmaals vouwen (vouwlijnen over elkaar), delen we die hoek van 180 graden
in twee hoeken van 90 graden.
 |
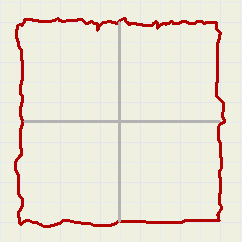
Bij uitvouwen heeft het blad twee loodrecht op elkaar staande (rechte) vouwlijnen gekregen.
 |
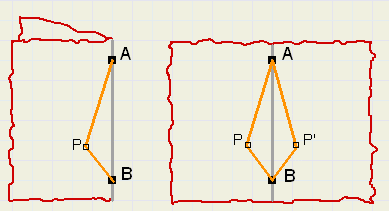
Waarom zou een vouwlijn recht zijn?
Teken op het uitgevouwen blad twee punten (A en B) op een vouwlijn.
Leg carbonpapier op het blad.
Vouw het blad samen en teken een route van A naar B , die buiten de vouwlijn loopt
bijvoorbeeld via het punt P. Vouw daarna het blad open.
Door het carbonpapier staan er twee routes van A naar B via P, die uiteraard even lang zijn.
Die route kan dus nooit de kortste zijn, want daar is er maar één van.
Alleen een punt op de vouwlijn blijft bij samenvouwen op zijn plek, levert geen extra
route op. De vouwlijn is de kortste verbinding.
 |
Overstaande- ,complementaire- en overeenkomstige hoeken
Bekijk de figuur hieronder:
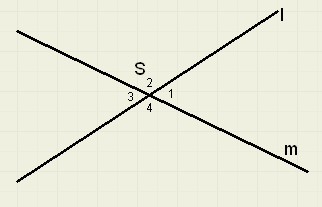 |
twee snijdende lijnen , l en m, leveren het snijpunt S op en vier hoeken,
die we 1,2,3 en 4 nummeren.
Opmerking: spreek L uit als "hoek".
In de figuur heten LS1 en LS3 overstaande hoeken.
Een ander paar overstaande hoeken is LS2 en LS4.
De hoeken LS1 en LS2 heten complementair,
omdat ze samen een hoek van 180 graden vormen.
Ook geldt: LS3 + LS4 = 180 graden,
zodat dit ook complementaire hoeken zijn.
Stelling
-
Overstaande hoeken zijn gelijk
-
zowel LS1 als LS3 hebben LS2 als complementaire hoek.,
zodat ze gelijk zijn.
Anders bekeken:
Draai de hele figuur 180 graden om snijpunt S, waarna alle lijnen weer op dezelfde plaats liggen
en de hoeken van plaats zijn gewisseld.
bekijk de figuur hieronder:
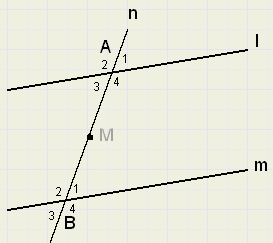 |
l en m zijn evenwijdige lijnen.
De lijn n snijdt l in punt A en m in punt B.
In de figuur heten LA1 en LB1 overeenkomstige hoeken.
Andere paren overeenkomstige hoeken zijn bijvoorbeeld LA2 en LB2
en ook LA3 en LB3
Stelling
-
Overeenkomstige hoeken zijn gelijk
-
Teken een punt M op het midden van lijnstuk AB.
Gebruik M als middelpunt, waar de gehele figuur om draait en draai 180 graden.
Daarna zijn A en B van plaats zijn gewisseld evenals de hoeken LA1 en LB3, die dus gelijk zijn.
Nu is ook LB3 = LB1, zodat inderdaad LB3= LA1
opmerking: een lijn die 180 graden draait om een punt, verandert niet van richting.
Anders bekeken:
Een hoek geeft richtingsverschil aan tussen lijnen.
Tussen evenwijdige lijnen is geen verschil van richting.
Zodat een derde lijn, die deze evenwijdige lijnen snijdt, gelijke hoeken maakt met elk ervan.
De hoeken LB1 en LA3 heten verwisselde binnenhoeken en ze zijn ook gelijk.
Het bewijs wordt aan de lezer overgelaten.
Bewijs 1.
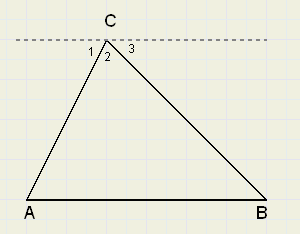 |
In de figuur zie je driehoek ABC. Door C is een hulplijn getrokken, evenwijdig aan AB.
Nu is:
-
LA = LC1....................verwisselde binnenhoeken
LB = LC3....................verwisselde binnenhoeken
zodat wegens
LC1 + LC2 + LC3 = 180 graden ook geldt:
LA + LB + LC = 180 graden.
Bewijs 2a.
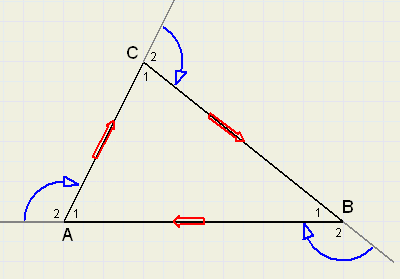 |
Startend op het nidden van AB varen we het rondje A,C,B.
Op het uitgangspunt teruggekomen is het bootje totaal 360 graden gedraaid, dat is de som van
de draaiingen bij A, C en B.
Dus:
-
LA2 + LC2 + LB2 = 360 graden.
Nu is (complementaire hoeken) :
LA2 = 180 - LA1
LB2 = 180 - LB1 en
LC2 = 180 - LC1
zodat
180 - LA1 + 180 - LB1 + 180 - LC1 = 360 graden
540 - (LA1 + LB1 + LC1) = 360 graden
LA1 + LB1 + LC1 = 180 graden..
Bewijs 2b.
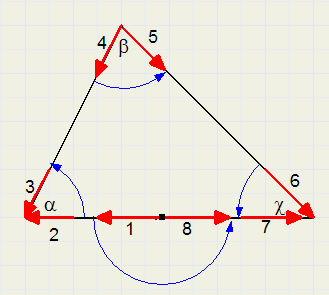
Het vorige bewijs kan nog worden vereenvoudigd.
In de figuur hieronder beweegt een pijl van positie 1. naar positie 8.
Daarbij draait de pijl 180 graden, precies de som van de hoeken van de driehoek.
 |
Bewijs 3.
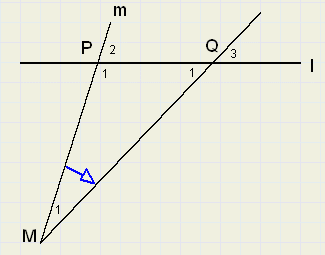 |
De lijnen l en m snijden elkaar in P.
Op m wordt een punt M gekozen en m verdraait om M over een hoek LM1.
Daardoor wordt Q het nieuwe snijpunt met l.
LP2 is het verschil in richting van lijnen l en m.
Na de draaiing is dat verschil kleiner geworden en wel met LM1
zodat
-
LQ3 = LP2 - LM1.
Nu is:
LP1 = 180 - LP2
LQ1 = LQ3
zodat
LM1 + LP1 + LQ1 = LM1 + 180 - LP2 + LP2 - LM1 = 180 graden.


