De Torens van Hanoi

load program
load complete Delphi-7 project

De Torens van Hanoi een bekende maar nog steeds leuke logistieke puzzel.
In dit artikel beschrijf ik een Delphi project waarmee je zelf oplossingen kunt zoeken.
Maar ook de computer kan de oplossing leveren.
Daarbij wordt een recursief algoritme gebruikt.

Het spel.

Bekijk eens het onderstaande plaatje:
6 stenen moeten één voor één worden verplaatst van A naar B.
Een steen mag daarbij nooit op een kleinere rusten.
Om dat te vermijden moet een derde (C) stapel worden gebruikt.

Voor slechts twee stenen is de procedure:
    1. verplaatst bovenste steen van A naar C
    2. verplaats steen van A naar B
    3. verplaatst steen van C naar B
zie plaatje:
Twee stenen vereisen 3 verplaatsingen.
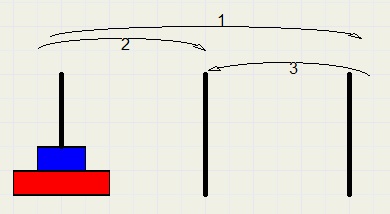
Hoeveel zetten (verplaatsingen) zijn nodig bij 3 stenen?
De truuk is om de twee bovenste stenen van A naar C te verplaatsen op eerder genoemde manier.
Verplaats dan de derde steen van A naar B.
Zet dan de twee stenen van C naar B.
We zien, dat dit 3 + 1 + 3 = 7 zetten vergt.

In het algemeen:
n stenen verplaatsen van A naar B vergt (n-1) stenen van A naar C,
één steen van A naar B en weer (n-1) stenen van C naar B.

Als n stenen in m zetten verplaatst kunnen worden dan kosten (n+1) stenen dus 2m+1 zetten.
n stenen verplaatsen kost 2n -1 zetten.

Bewijs:
Neem aan dat bovenstaande formule voor n juist is.
Dan vragen (n+1) stenen dus 2n+1 – 1 zetten (vervang gewoon n door n+1).
Maar er geldt natuurlijk ook: 2. (2n -1) + 1 zetten maar dit is gelijk aan de vorige formule.
Omdat de formule klopt voor n=1 klopt hij ook voor n=2, dus ook voor n=3 enzovoorts.

Opmerking: dit type bewijs heet “inductie”.

Het algoritme

De kracht van computers bevindt zich in de herhaling van code.
Dat kan op verschillende manieren.
We kennen subroutine calls, in Delphi bekend als procedures en functies.
Ook zijn er loops (lussen).
De lokale variabelen van functies en procedures bevinden zich op het stack.
Elke nieuwe aanroep van een procedure heeft zodoende zijn eigen lokale variabelen.

Welnu, binnen functies en procedures zijn er twee methodes om code te herhalen:
    1. met loops (iteratie genoemd)
    2. met recursie
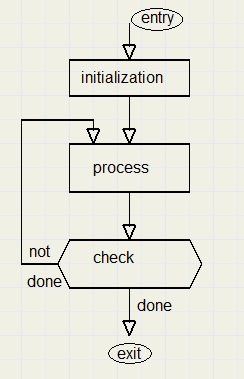
In het algemeen ziet een loop er zo uit:
Gedurende de initialisatie worden variabelen op een beginwaarde gezet (meestal 0)
De test (van een variabele) bepaalt of de het proces wordt herhaald of de procedure wordt verlaten.

Recursie betekent dat de procedure (of functie) zichzelf opnieuw aanroept.
Dat is verwarrend, dus voor de duidelijkheid dupliceren we even de procedure.
Dat levert op in geval van procedure Proc met parameter a:
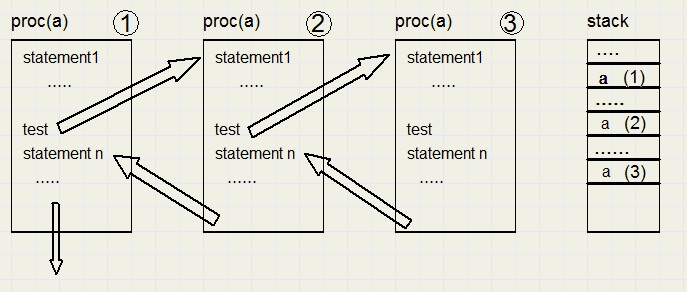
Parameter a is verschillend per aanroep!
Uiteraard is een test nodig om te beslissen of de procedure zichzelf moet aanroepen
dan wel de overige code moet uitvoeren.

Nu terug naar de Torens van Hanoi.
We geven waardes 1,2,3 aan de stapels A,B,C.
Als we een steen verplaatsen van (1) naar (2) dan is de reserve stapel gelijk aan 1 xor 2 = 3.
Bij verplaatsing van (2) naar (3) is de reserve stapel 2 xor 3 = 1. Handig!

Stel we moeten n stenen verplaatsen van stapel p1 naar stapel p2.
We bouwen de procedure 
procedure solveGame(p1,p2,n : byte);
//move n stones from pile p1 to p2
var p3 : byte;
begin
 if resetFlag then exit;
//
 if (n = 1) then
  begin
   reportmove;
   movestone(p1,p2);        //1 stone to move
  end
  else
   begin
    p3 := p1 xor p2;        //more than 1 stone to move
    solveGame(p1,p3,n-1);
    solveGame(p1,p2,1);
    solveGame(p3,p2,n-1);
   end;
end;
Dat is alles!
Per procedure aanroep verschijnen p1, p2, p3 apart op het stack.

Opmerkingen:
resetFlag wordt op true gezet door een klik op de RESET knop.
De reset aktie wacht tot de kraan tot stilstand is gekomen.
Reportmove schrijft een boodschap in het form om de voortgang weer te geven.
p1,p2,p3 zijn de stapels.

Voor het verplaatsen van 6 stenen van stapel 1 naar stapel 2 is deze simpele aanroep genoeg:
SolveGame(1,2,6);
Blijft over de vraag: wat doet procedure movestone ?

Het programma

Hieronder staat een iets verkleind plaatje van het programma in werking: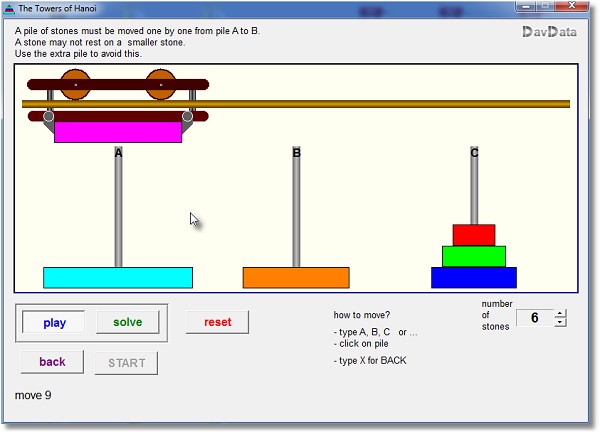
Er zijn twee modussen:
    play: de speler zoekt naar oplossingen.
    Solve : de computer zoekt naar een oplossing.

RESET forceert het spel in de startpositie met alle stenen op stapel A.

Programma structuur

Het project heeft 2 units en een form:
    - unit1 : game control, event handling
    - game-unit : tekenprocedures voor het spel met de kraan-bewegingen
    - form1 : paintbox voor het tonen van het spel en knoppen voor controle
Tekenen geschiedt in een bitmap, die later naar de paintbox wordt gekopiëerd.

De tekenprocedures nemen het merendeel van de code voor hun rekening.
De kraan voor de stenenverplaatsing is puur voor de lol toegevoegd.
Deze kraan hangt aan een rail,
de delen boven en onder de rail worden door afzonderlijke procedures getekend.
Het bovenste deel kan alleen horizontaal bewegen, het onderste deel ook vertikaal.
De teken procedures zijn in drie levels verdeeld.
Level 1 procedures roepen level 2 aan, level 2 procedures level 3 om een klus te klaren.

level 1 paint procedures/functies:

function LoadStone(p : byte) : boolean;
    pakt de bovenste steen van stapel p
    exit true als OK, false als de stapel leeg is

function unloadStone(p:byte) : boolean;
zet de opgepakte steen op stapel p
    exit true als OK, false als stapel p reeds een kleinere steen bevat

procedure movestone(p1,p2 : byte);
    roept loadstone( ) en daarna Unloadstone( ) aan
    alleen gebruikt door computer search

level 2 paint procedures/functies

procedure erasePile(p : byte);
procedure paintPile(p : byte);
    wis/teken stapel p (1,2,3) met alle stenen

procedure moveCraneHor(pos : word);
procedure moveCraneDown(posY,clampPos : word);
procedure moveCraneUp;
    beweeg kraan naar pixel positie pos (of posY, vertikaal)
    clampPos is de horizontale positie van de grijparmpjes, die moeten zich instellen
    op de breedte van de te grijpen steen.

level 3 paint procedures/functies (enkele)

procedure paintCraneRail;
procedure paintcranewheels;
procedure paintWheelJoint;
procedure paintUpperCrane;
procedure paintlowerCrane;
procedure paintCraneLoad;
procedure paintstoneRect(r : Trect; stoneNr : byte);

Er zijn er nog wat meer om bijvoorbeeld pixel posities van stenen of de kraan te berekenen.
Kijk a.u.b. naar de source code voor details.

Variabelen in de game_unit:

var map : Tbitmap;
    game : array[1..3,1..maxheight] of byte;
    pheight : array[1..3] of byte;//number of stones of pile
    stonecount : byte;
    cranePosX : word;
    cranePosY : word;
    craneLoad : byte; //0:no load 1..6:loaded with stone ..
    cranePile : byte;
    clampBase : word;
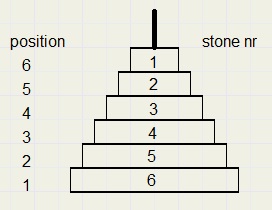
De stenen hebben een nummer afhankelijk van hun grootte.
1 is de kleinste, 6 de grootste.
Game(2,1) = 5 wil zeggen dat stapel 2 een steen van grootte 5 bevat op positie 1.

StoneCount is het aantal stenen in het hele spel, te veranderen met een UPDOWN control op form1.

De figuur hieronder toont de stenen op stapel A bij de start:
Hiermee besluit ik dit artikel over de Torens van Hanoi.

Toevoeging: Waarom ik recursie niet zo handig vind

Want op het eerste gezicht is de compacte code verbazingwekkend.
Maar als eerste nadeel blijkt zulke code lastig te begrijpen.
Ten tweede is het proces amper te besturen. Er kan niet tussentijds worden gestopt of hervat.
Om de computer te stoppen moet een truuk worden ingebouwd:
de resetRequest flag forceert exits , wat niet erg elegant is.
Een betere manier zou zijn om een array te maken met verplaatsingscodes
en die codes daarna één voor één uit tevoeren.
Dan kan de speler volledige controle houden, het zoekproces onderbreken,
het zelf overnemen of zetten terugnemen. Nu kan dat allemaal niet.