Grafieken en Vergelijkingen

Dit artikel gaat over bewerkingen op vergelijkingen en grafieken.
Cirkels en ellipsen dienen hierbij als voorbeeld.
Eerst wat begrippen:

variablemeestal x of y, een getal dat verschillende waarden kan aannemen
constanteeen vaste waarde, bv. 3, -5 maar ook a, b of x1, y1
formuleeen berekening waarin variabelen voorkomen
vergelijking een uitdrukking van de vorm: formule = formule

Een functie is een speciale vorm van een vergelijking namelijk
    y = ...x.....
Links van het "=" teken staat één variable, het resultaat van de berekening, met x rechts van het "=" teken.
de "..." staan voor bewerkingen en constanten.
X heet hier de onafhankelijke- en y de afhankelijke variabele.
x krijgt een waarde en het resultaat van die berekening met x is y.
Omdat een functie één getal als resultaat oplevert kunnen functies weer onderdeel zijn van een formule.

Voorbeelden van formules zijn:
3x2 + 5y2
7x - 8y - 10.

Voorbeeld van een vergelijking is:
3x2 + 5y2 = 2x - y + 25

Voorbeelden van functies zijn:
y = 3sin(x)
y = 3x3 - 2x2 + x - 7

Grafieken

Grafieken zijn afbeeldingen van vergelijkingen of functies.
Neem de vergelijking x2 + y2 = 1

Voor een waarde van x kan y worden berekend.
Zetten we die x en y waarden waarvoor de vergelijking klopt bij elkaar als (x,y) dan
kunnen we voor elk (x,y) paar een punt zetten in een coördinatenstelsel.
Voor het bovenstaande geval zien we dan voor alle punten (x,y) dit:



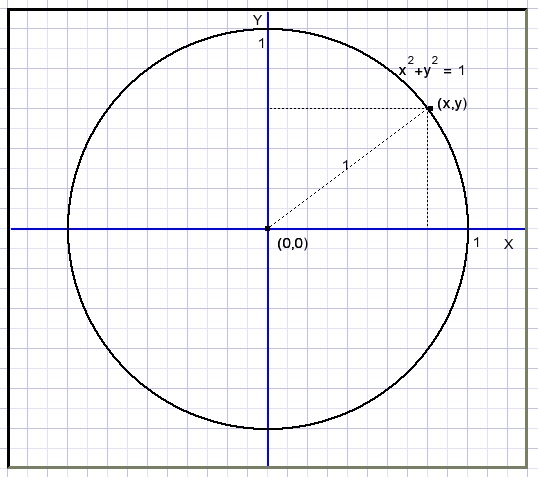
Een cirkel met (0,0) als middelpunt en een straal van 1.
De stelling van Pythagoras toont aan waarom.

Verschuiven

Het middelpunt zou ook op een andere plaats dan de oorsprong kunnen liggen.
Hoe verandert de vergelijking dan?
We pakken het verschuivingsprobleem algemeen aan.

Stel dat een grafiek de vergelijking ..x..y.. = ..x..y.. heeft en dat (x1,y1) op de grafiek ligt.
Nu vervangen we (x) door (x+1) en (y) door (y+2).
Dat levert ..(x+1)..(y+2) = ..(x+1)..(y+2)
Stel dat een punt (x2,y2) op die verschoven grafiek ligt.
Dat is het geval als geldt:
    (x2 + 1) = x1
    (y2 + 2) = y2
immers, de vergeliking klopte voor (x1,y1)
oftewel:
    x2 = x1 - 1
    y2 = y1 - 2
In een plaatje:



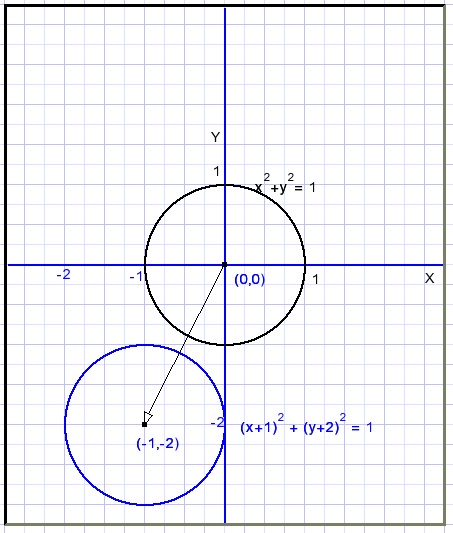
De grafiek is 1 naar links en 2 naar beneden geschoven.
Algemeen, als in een vergelijking :
    x wordt vervangen door (x+h) dan schuift de grafiek h naar links.
    y wordt vervangen door (y+v) dan schuift de grafiek v omlaag.

Opmerking : Voor negatieve waarden van h en v schuift de grafiek naar rechts en omhoog.

Dit geldt voor alle functies en vergelijkingen.

Verschuiving en vergelijking
We gaan weer uit van cirkel x2+y2=1 en vervangen (x) door (x+h) en (y) door (y+v).
Dat levert:
    (x+h)2 + (y+v)2=1
    x2+2hx+h2+y2+2vy+v2=1

Aan de factoren van de kwadraten van x en y verandert niets.
Wel nieuw is de verschijning van de termen 2hx en 2vy.
Daaraan is direct de verschuiving af te lezen.

Voorbeeld
x2-10x+y2+6y=47 is een verschoven cirkel.
    2h = -10.....h = -5.....verschuiving van 5 naar rechts.
    2v = 6.......v = 3......verschuiving van 3 omlaag.

Uitrekken

In de vergelijking x2+y2 = 1 vervangen we x door x/2.
Wat is het effect?
Stel (x1,y1) ligt op de cirkel en na vervanging van x door x/2 is dat punt (x2,y2) geworden.
Dan moet gelden:
    x2/2 = x1
    oftewel
    x2 = 2x1


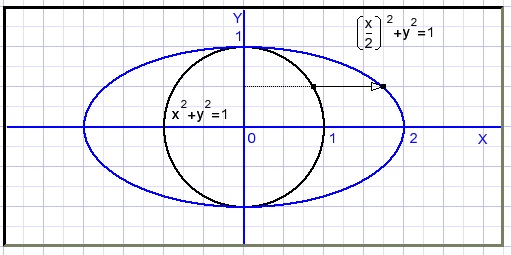
Het effect is uitrekking van de cirkel met een factor 2 in horizontale richting.
Zo'n uitgerekte cirkel heet een ellips.

Algemeen, als in een vergelijking:
    x wordt vervangen door (x/a) dan rekt de grafiek een factor a horizontaal uit.
    y wordt vervangen door (y/b) dan rekt de grafiek een factor b in vertikale richting uit.
Opmerking: voor een factor < 1 is dat krimp.

De algemene vergelijking van een ellips:



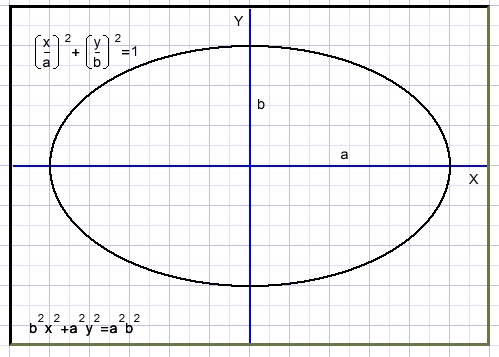
Uitrekken en de vergelijking
De cirkel x2 + y2 = 1 wordt na uitrekking met een factor a horizontaal en b vertikaal (x/a)2 + (y/b)2 = 1.
Door vermenigvuldiging met a2b2 ontstaat de vergelijking b2x2 + a2y2 = a2b2
Uitrekken verandert de factoren van de kwadraten en de constante term zonder x of y.
Er komen geen andere termen bij.

Voorbeeld
Gegeven is de ellips: 9x2+49y2 = 441.
Bepaal "a" en "b".
Deel beide termen door 441 :



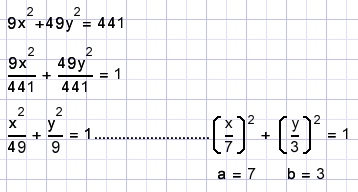
Rotatie

We roteren punt P(x1,y1) tegen de klok in over een hoek φ
Om te zien wat het effect is beschouwen we x1 en y1 afzonderlijk.



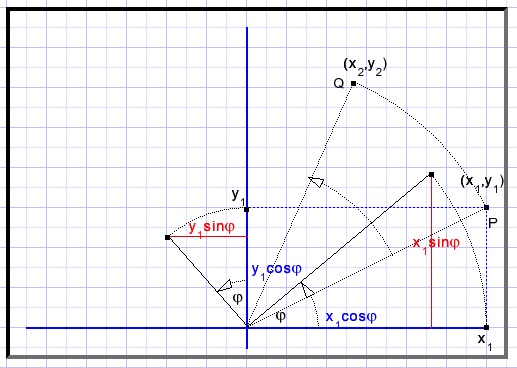
Q is het geroteerde punt P.
Het rotatie middelpunt is de oorsprong (0,0).

De rotatie van x1 levert
    x2 = x1cosφ
    Δy = x1sinφ.......de invloed x op y
De rotatie van y1:
    y2 = y1cosφ
    Δx = y1sinφ........de invloed y op x
De resultaten bij elkaar geteld:
    x2 = x1cosφ - y1sinφ
    y2 = y1cosφ + x1sinφ
Algemeen:
Als in een vergelijking met x en y :
    (x) wordt vervangen door xcos(φ)-ysin(φ)
    (y) wordt vervangen door ycos(φ+xsin(φ)
dan zal de grafiek φ graden naar rechts roteren.
(Immers: de (x,y) waarden waarvoor de vergelijking klopt worden bereikt na rotatie linksom over een hoek φ)

Rotatie en vergelijking
De ellips b2x2+a2y2 = a2b2 draaien we φ graden rechtsom.
Het rotatie middelpunt is (0,0).
De vergelijking verandert in
    b2(xcosφ - ysinφ)2 + a2(ycosφ + xsinφ)2 = a2b2.
Als we deze vergelijking uitschrijven zonder de haakjes dan zien we termen met xy verschijnen
    -2b2xysinφcosφ
    2a2xysinφcosφ
daaraan is een rotatie te herkennen.
Rotatie verandert ook de factoren van de termen met x, y, x2, y2 en de constante term.

Voorbeeld
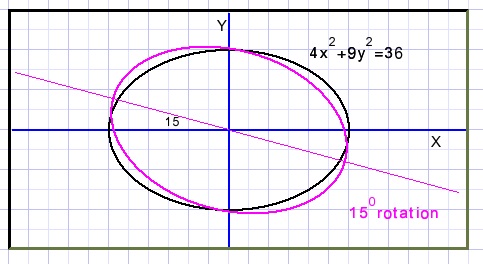
Ellips 4x2 + 9y2 = 36 wordt geroteerd.
In de nieuwe vergelijking komt de term 2,5xy voor.
Vraag: over welke hoek vond rotatie plaats?
    b = 2.
    a = 3.
    2(a2 - b2)sinφcosφ = 2,5
    10sinφcosφ = 2,5
    2sinφcosφ = 0,5
    sin(2φ) = 0,5
    φ = 15



Voorbeeld
Gegeven is de ellips: 2x2+y2 = 2(x + y + xy -1 ).
Hieronder de grafiek:



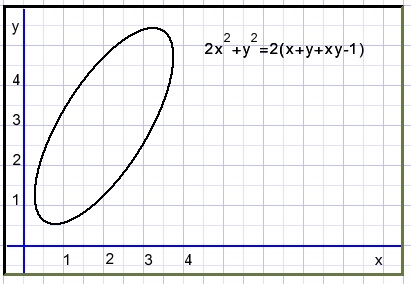
De x,y termen zijn gevolg van de verschuiving, de xy term van rotatie.
Maar hoeveel?
Eerst eens de grafiek verschuiven zodat de x en y termen verdwijnen.

x vervangen we door (x+h) en y door (y+v).
Dat levert twee vergelijkingen op waarmee wij h en v berekenen zodat de x en y termen verdwijnen.
    2(x+h)2 + (y+v)2 = 2(x+h) + 2(x+v) +2(x+h)(y+v) -2
    Vis hieruit de termen van x en y :
    x termen: 4h = 2 + 2v
    y termen: 2v = 2 + 2h
    Vereenvoudigen:
    2h - v = 1
    v - h = 1
    Oplossing:
    h = 2
    v = 3
Dat komt overeen met wat de grafiek toont.
De vergelijking wordt, na verschuiving van 2 naar links en 3 omlaag:
    2(x+3)2 + (y+2)2 = 2[x+3 + y + 2 + (x+3)(y+2) - 1]
    na vereenvoudiging:
    2x2 + y2 - 2xy = 3
Welke rotatie vond plaats? Welke afmetingen heeft de ellips?

werkwijze om de rotatie te bepalen
We gaan uit van de algemene formule van de ellips

Maar rechts van het "=" teken kan natuurlijk een ander getal staan dan 1.
Dat betekent dat eigenlijk a en b iets veranderd worden.
Ook zagen we hiervoor, dat rotatie alleen a en b verandert en een term met xy toevoegt, constanten wijzigen niet.
In de vergelijking b2x2 + a2y2 = a2b2 is de term rechts van het "=" teken het product van de factoren van x2 en y2.
Waarom deze verhandeling?
We gaan onderzoeken 2x2 + y2 - 2xy = 3
Rechts van het "=" teken staat geen 1 maar een drie. Straks meer over deze valkuil.

Als we stellen
    p = cosφ
    q = sinφ
Dan roteren we een grafiek φ graden rechtsom als
    (x) wordt vervangen door (px - qy)
    (y) wordt vervangen door (py + qx)
We gaan deze bewerking op de standaard vergelijking van een ellips loslaten.
Dat levert dan een nieuwe vergelijking op met andere factoren voor de x2, y2 en xy termen.
Deze factoren stellen we gelijk aan die in 2x2 + y2 - 2xy.
Dat levert een stelsel vergelijkinegn op (met a,b,p,q) waaruit a,b,p,q hopenlijk zijn op te lossen.
a,b zijn dan de afmetingen van de niet geroteerde ellips en p,q bepalen de hoek van de rotatie.

De berekende a,b zijn echter afgeleid voor de vergelijking ....= 1.
De vergelijking waar we mee werken laat zien ....= 3.
We moeten dus uitgaan van de vergelijking b2x2 + a2y2 = 3a2b2.



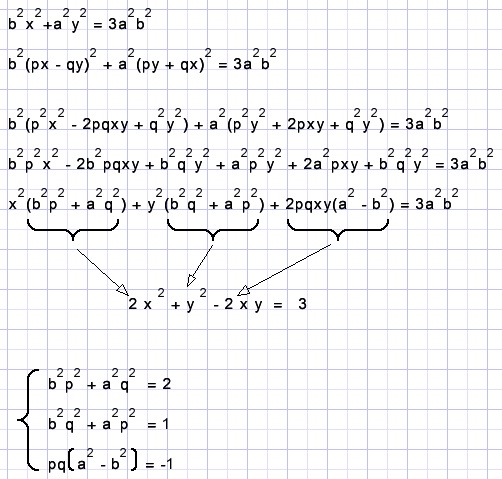
Ziehier het stelsel vergelijkingen dat opgelost moet worden.
p2 + q2 = 1 had daar nog bij kunnen staan.
Eerst bepalen we p en q.
We trekken de tweede regel af van de eerste en voegen de termen met p2 en q2 samen:



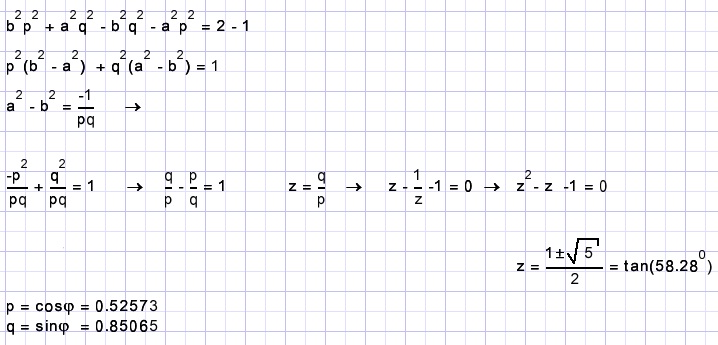
Opmerking: φ is de rotatiehoek. z = tanφ

Resteert het bepalen van a en b.
We gaan weer van het stelseltje van 3 vergelijkingen uit.
Nu tellen we regels 1 en 2 bij elkaar op en plaatsen weer p2 en q2 buiten haakjes:



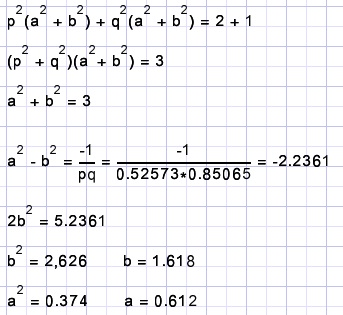
Rechts van het "=" teken komt 3a2b2 = 2,946.
De ellips had voor de rotatie en verschuiving de vergelijking:



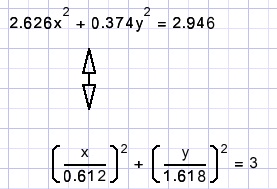
Het volgende plaatje laat het allemaal zien:



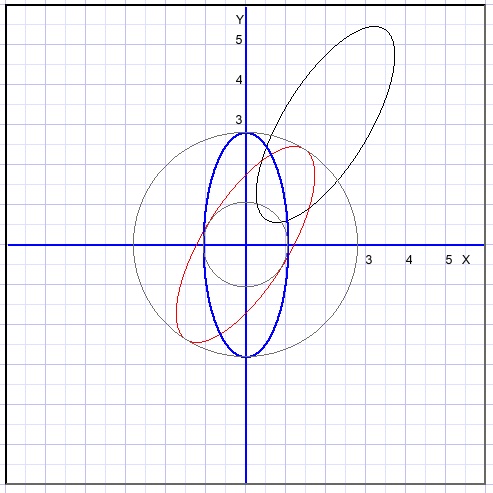
Voor de duidelijkheid zijn twee cirkels met straal a en b toegevoegd.

Zelf aan de slag

We begonnen met de vergelijking 2x2+y2 = 2(x + y + xy - 1)
Maar ook te onderzoeken zijn andere vergelijkingen zoals nx2+y2 = 2(x + y + xy - 1) voor n = 3,4,...
Het volgende probleem trof ik aan in een Facebook wiskunde groep:
los op de vergelijking
    5x2+y2 = 2(x + y + xy - 1)
Dat lijkt een rare vraag want op het oog staat hier de vergelijking van een geroteerde en verschoven ellips.
Er blijkt echter maar één oplossing te zijn voor x en y.
Plotten van deze vergelijking toont maar één punt.
Welk?