Delphi globe project

Een Roterende Wereldbol

Downloads

Er zijn twee Delphi-7 projecten:

		download program 1			download complete Delphi project 1
		download program 2			download complete Delphi project 2

Introductie

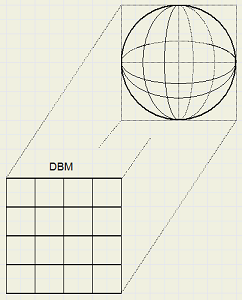
Dit artikel beschrijft de constructie van een globe uitgaande van een 2:1 cilindrische projectie.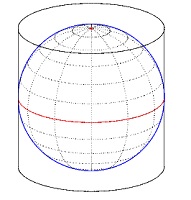

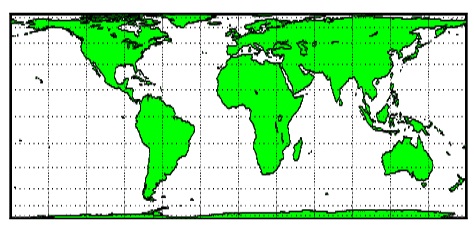Om de wereldbol is een cilinder gevouwen.
De vertikale cirkelbogen op de globe worden de vertikale lijnen op de cilinder.
Dan wordt de cilinder uitgevouwen en het resultaat zien we rechts.
De breedte van die rechthoek is p x globe diameter.
De hoogte is de helft van die waarde.
Op de evenaar is de pixelgrootte gelijk aan die op de globe, maar hoger of lager worden de pixels horizontaal uitgerekt.

Dit Delphi project tekent een globe uitgaande van de projectie voorziet ook in het roteren van de globe.
Het kost 3 milliseconden om een globe te construeren.
Afmetingen van de rechthoek zijn 756 * 378, diameter van de globe is 240 pixels.
Dit project bevat tevens debug informatie, zichtbaar gemaakt op het form.

Hierna is een nieuw project gemaakt dat uitgaat van een projectie met afmetingen 2700 * 1350
en een globe diameter van 860 pixels. Maar daar gaat dit artikel niet over.

Hoe het werkt

Uit de 2:1 projectie wordt eerst een 1:1 rechthoek gekozen.
Rotatie ontstaat door steeds een iets ander gebied te kiezen.
Dit vierkant wordt geplaatst in bitmap SBM (source bitmap).
De globe wordt afgebeeld in bitmap DBM (destination bitmap).
Daarvoor worden de pixels van DBM gescanned van links naar rechts, boven naar onder.
Een vooraf berekende tabel, CCT (coördinaten conversie tabel) , levert voor elk DBM pixel een rechthoekje op SBM.
De pixel kleuren in deze rechthoek worden gesommeerd en de gemiddelde waarde berekend.

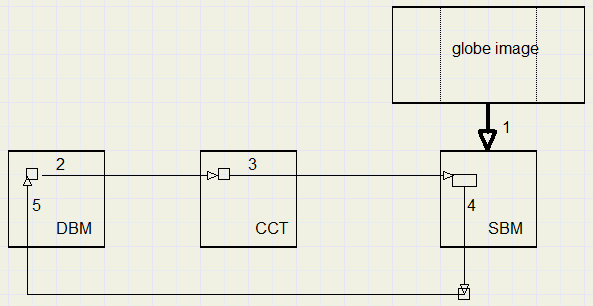
De CCT bedekt slechts het kwadrant in de linker tophoek van de bitmaps.
De coördinaten in andere kwadranten zijn simpel te berekenen uit de symmetrie t.o.v. de horizontale en vertikale middellijnen.

Hieronder staat een verkleinde tekening van de CCT waarden.
Elk rechthoekje levert een pixel van de globe.

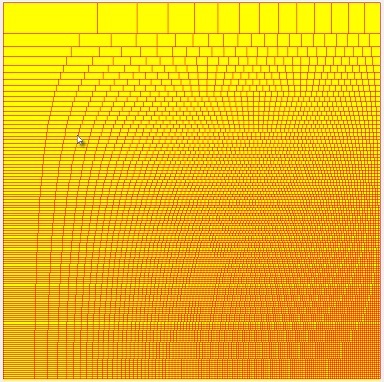
Tot zo ver de algemene beschrijving. Tijd voor de details.

Constructie van de CCT (coordinate conversion table)

Het originele projectie bestand heeft afmetingen 756 x 378 pixels.
The SBM heeft 378 x 378 pixels.
Deze pixels kwamen oorspronkelijk uit de vertikale cirkelbogen op de globe,
dus de diameter van de oorspronkelijke globe was 756 / p = 240.6 pixels.
We kiezen een destination bitmap (DBM) met 240 * 240 pixels.
De CCT telt dus 120 x 120 pixels, het kwadrant links boven.
Dit project is geschreven met voornoemde afmetingen als constanten.
Vandaar een nieuw project met een veel grotere globe.

Vanuit de DBM kijken we via parallelle lijnen naar de globe.
De breedtegraden zien we dan als horizontale lijnen evenwijdig aan de evenaar.
De lengtegraden zien we als ellipsbogen.
Eerst leggen we het verband tussen een vertikale DBM pixel coördinaat en de SBM.

De vertikale coördinaat op de SBM is ys (y source).

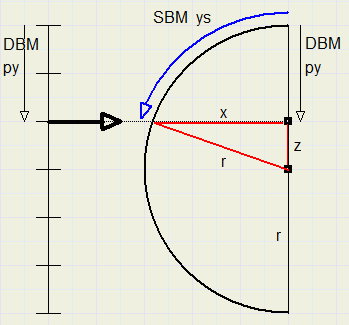
Variabelen x,r,z dienen alleen voor deze beschrijving. In het Delphi project heten ze anders.

Voor een bepaalde py waarde van een DBM pixel berekenen we
z = r – py
X = sqrt(r^2 – z ^2)
ys = r . arctan(x / z)

Bedenk, dat een arctan functie de hoek in radialen levert.
Bij een hoek hoort dan een cirkelboog die gelijk is aan straal * hoek.
( 2p radialen = 360 graden)

Uiteraard moet de waarde van ys op hele getallen worden afgerond omdat het een SBM y coordinaat is.
Hierna moeten we het verband berekenen tussen de horizontale coördinaat van een DBM pixel en de SBM.

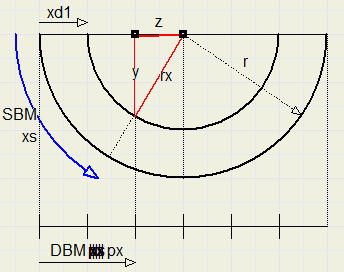
Uitgaande van DBM pixel px horizontaal berekenen we :
z = r – px
rx = r – xd1 ( xd1 = 120 – x , zie plaatje met sy berekening)
y = sqrt(rx^2 – z^2)
xs = r . arctan(y / z)
Ook hier moet xs op een geheel getal worden afgerond.

Dit is de theorie. De rechthoekjes op SBM worden verkregen door opvolgende waarden (xs,ys) uit de CCT te halen.

De kleuren

Hele pixels pakken uit de SBM geeft een grof resultaat.
Voor vloeiende kleurovergangen kunnen we met floating point getallen rekenen maar hier kiezen we een compromis.
Een pixel wordt opgevat als 16 (4 * 4) subpixels.
Dit is simpel te verwezenlijken door de coördinaten met 4 te vermenigvuldigen.
De twee laagste bits selecteren dan het horizontale- of vertikale subpixel 0,1,2, of 3.
Vermenigvuldigen met vier is 2 naar links schuiven. (shl 2)
Vertragende floating point berekeningen worden zo vermeden.

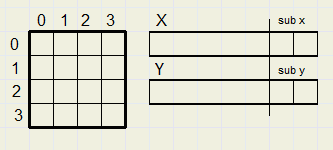
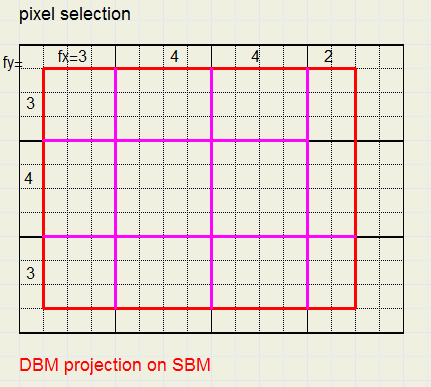
De rode rechthoek is de projectie van een DBM pixel op de SBM.
Cf = fx . fy is het aantal subpixels per pixel.
Deze waardes worden gesommeerd in variable cfs = cfs + cf.
De pixel kleuren worden opgeteld in variabelen colR, colG, colB voor respectievelijk rood, groen en blauw.
ColR = colR + cf . PixelColor etc.
De uiteindelijke gemiddelde rode kleur is ColR / cfs.

Kleur extractie uit een pixel.

Windows heeft dit formaat voor de kleur van een pixel:

Echter, binnen een bitmap zijn er een aantal verschillende formaten.
Het makkelijkst is het formaat pf32bit (property: pixelformat) dat er zo uitziet:

De rode en blauwe 8 bits velden zijn van plaats gewisseld.

Wegens de snelheid gebruiken we de relatief trage property pixels[ , ] niet.
Inplaats daarvan lezen we pixels direct uit het geheugen. Dat is minstens 50 keer zo snel.

Een bitmap kent de property scanline[n] die het geheugen adres geeft van het meest linkse pixel op lijn n.
Dit adres wordt bewaard als dword ( = cardinal) variabele om berekeningen te vergemakkelijken.
Voor bitmap DBM bepalen we twee waarden:
1: DBM0 = dword(DBM.scanline[0]
2: DBMstep = DBM0 – DBM.scanline[1]

Ook is er data type P32:
type P32 = ^dword

Net zo is er voor bitmap SBM: SBM0 en SBMstep.

De opdracht color := pixel[x,y] kan nu worden vervangen door:

addr := SBM0 – y*SBMstep + (x shl 2)
color := P32(addr)^

Het extraheren van de kleuren uit het pixel dword gaat zo:

colR := color shr 16; //red
colG := (color shr 8) and $ff; //green
colB := color and $ff; //blue

Procedure MakeSphere;
Hier de algemene structuur, loops binnen elkaar:
--------------------------------------------------------------------
by stapt 1..119 door de pixel rijen van DBM  (by:base y value)
  bx stapt xd1..119 door de pixel kolommen van DBM   

  { (hx1,hy1)..(hx2,hy2) definiëren de SBM rechthoek
    (hx = home value x)}

    q telt 1..4 om het kwadrant aan te geven

    {(px,py) zijn berekend uit (bx,by) om het DBM pixel te 
      adresseren}  
         {(x1,y1) en (x2,y2) zijn berekend uit (hx1,hy1) (hx2,hy2)       
      en geven het SBM subpixel}

    {(sx1,sy1) , (sx2,sy2) zijn de echte pixels posities op SBM}

         j telt pixels sy1 .. sy2  op de SBM

            i telt pixels sx1 to sx2 op de SBM

               {tel pixelkleuren op in colR, colG, colB}

          eind van  j,i loops     

           {bereken de DBM pixelkleur en bewaar die in (px,py)}

          einde van de q loop
     einde van de bx loop
einde van de by loop

---------------------------------------------------------------------------------

Debug informatie

Programmeren is doorlopend fouten maken.
Het is zaak voortdurend alles te controleren op juistheid.
Kijkend naar de globe zien we een cirkel. Pixels buiten deze cirkel moeten we negeren.
Hoe teken je een nette cirkel?
Onze cirkel beelden we ter controle af in paintbox3 (dimensie 240 * 240)
Hieronder een wat vergrote weergave.

Het programma gebruikt deze code, waarin i de positie van een horizontale lijn is.
Merk op, dat de bovenste lijn niet wordt ingevuld. Dat zou anders een raar uitstekend puntje opleveren.

for i := 1 to 119 do
 with CCT[i] do
  begin
   r := sqrt(14400-sqr(i-120));
   xd1 := round(120-r);
  end;//for i

xd1 is het meest links pixel op de cirkel van lijn i.
14400 is het kwadraat van 120, de straal van de cirkel.
We herkennen hier de stelling van Pythagoras.

In painbox2 op form1 tekenen we de layout van de CCT. Zie eerdere afbeelding.
Elk rechthoekje levert een bit per kwadrant in de DBM.

type TCC  = record
             xd1 : smallInt;     // x start on dest map
             ys  : smallInt;     // y position on source *4
             xs  : array[0..119] of smallInt; //x position *4                    
            end;

var sbm,dbm : Tbitmap;
    CCT : array[0..119] of TCC;
    HRpos : smallInt;        //horizontal center on source map
    dbm0,sbm0 : dword;       //location of [0.0]
    dbmstep,sbmstep : dword; //step down to next line

Als de muis over paintbox2 wordt bewogen dan verschijnt de bijbehorende CCT informatie in statictext components op form1.

Rotatie

Bitmap SBM is een vierkant en de kopie van een gedeelte van image1:

procedure buildSbm;
//build source bitmap from globe image
//use HRpos to select part of image = 756 * 378
var r,s : TRect;
begin
 with form1.image1.Picture.bitmap do
  begin
   s.Top := 0; s.Bottom := 378; r.Top := 0; r.Bottom := 378;
   if HRpos <= 378 then
    begin
     s.Left := Hrpos; s.Right := s.Left + 378;
     r.Left := 0; r.Right := 378;
     sbm.Canvas.CopyRect(r,canvas,s);
    end
    else
     begin
      s.Left := Hrpos; s.Right := 756;
      r.left := 0; r.Right := 756-HRpos;
      sbm.Canvas.CopyRect(r,canvas,s);
      r.left := r.Right; r.Right := 378;
      s.Left := 0; s.Right := HRpos-378;
      sbm.Canvas.copyrect(r,canvas,s);
     end;
  end; 
end;

Als de selectie over een linker- of rechter rand gaat, dan zijn twee kopiën nodig
om in de SBM het gewenste deel van de globe te krijgen.
De kopie gaat steeds van rechthoek s op het image naar r op de SBM.

Het lastigste deel van het programma is wel de berekening van de CCT.
Hier en daar duikt een magisch getal op maar bedenk dan, dat we steeds hoeken berekenen
en die met een straal vermenigvuldigen om een booglengte te krijgen.
En deze waardes zijn vermenigvuldigd met 4 omdat we tellen in subpixels voor vloeiende kleur overgangen.

Dit is een goed moment om de beschrijving te besluiten.
Voor verdere details verwijs ik naar de source code.

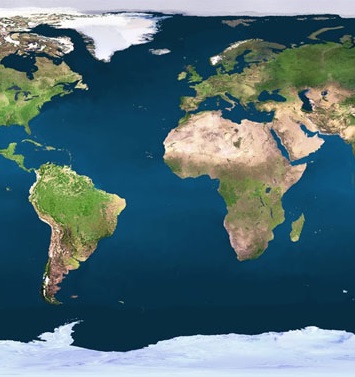
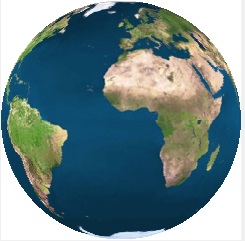
Als laatste hieronder nog een SBM links en DBM rechts.