Meetkunde probleem (50)

Opgave

Toon aan dat in de volgende figuur geldt: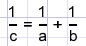



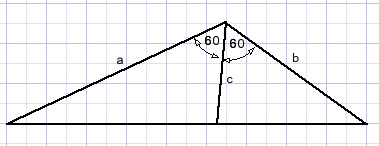
Oplossing 1

Deze oplossing berust op de deellijnstelling:
    "de deellijn van een hoek verdeelt de overstaande zijden in delen die zich verhouden als de aanliggende zijden"


Oplossing 2

Deze oplossing berust op oppervlakten
    [ADC] + [DBC] = [ABC]
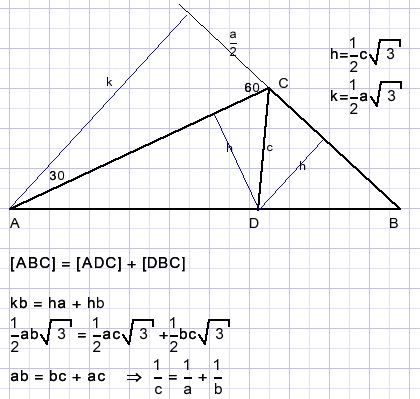
Opm. met [ABC] bedoel ik de oppervlakte van driehoek ABC



Oplossing 3

Deze oplossing berust op de stelling uit de goniometrie:
    "als twee lijnstukken a en b een hoek α maken dan is de oppervlakte van de ingesloten driehoek 0,5absin(α)"


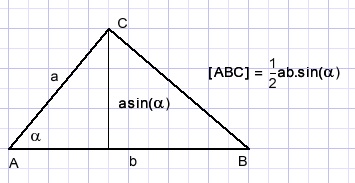
zodat (zie originele driehoek bovenaan pagina)
0,5ab.sin(120) = 0,5bc.sin(60) + 0,5ac.sin(60)
Omdat sin(120) = sin(60)
ab = bc + ac etc.

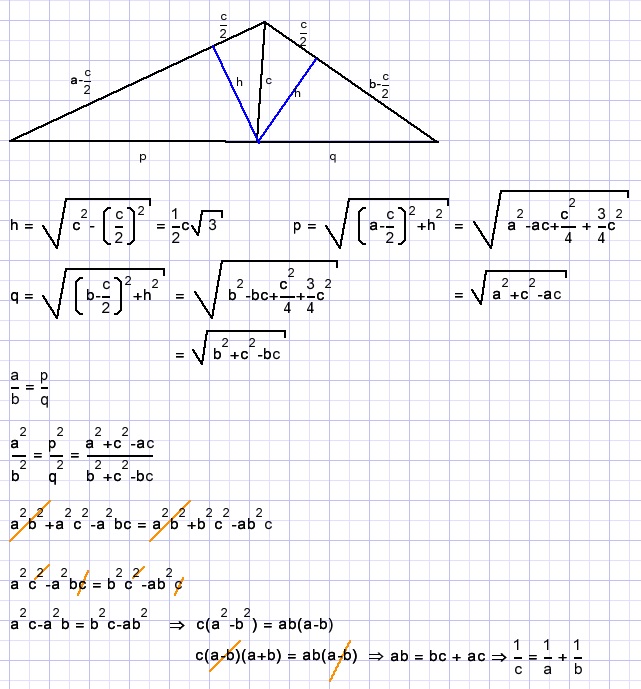
Oplossing 4

Deze oplossing berust op gelijkvormige driehoeken.