meetkunde probleem

Meetkunde probleem (48)

Opgave

Gegeven is vierhoek ABCD met aangegeven hoeken.
BC=DC.
Bereken de grootte van hoek x.

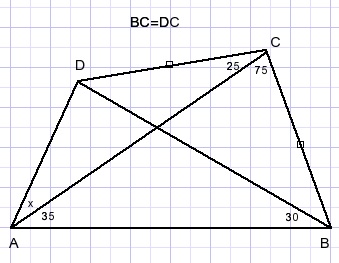
Oplossing

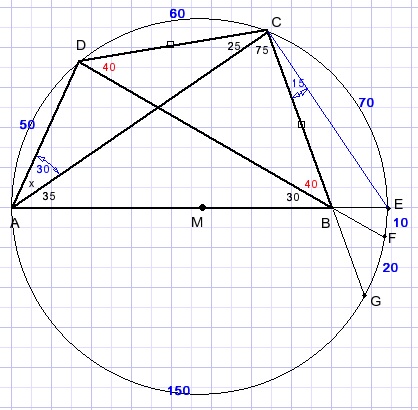
Construeer de omgeschreven cirkel van ΔACD.
Punt E is snijpunt van de cirkel met het verlengde van AB.
Punt F is snijpunt van de cirkel met het verlengde van DB.
boogAD = 2*25 = 50.
boogAG = 2*75 = 150.
boogCE = 2*35 = 70.
LCDB = LDBC = (180-(25+75))/2 = 40.
boogCF = 2*40 = 80.

Zo te zien is AE middellijn van de cirkel. M is het middelpunt.
Hiervan uitgaand is:
LBCE = 90-75=15.
boogGE = 2*15 =30.
LABC = 70 = (boogAC + boogGE)/2.
boogAC = 110.
boogDC = 110-50 = 60.
x = 60/2 = 30 graden.

Resteert te bewijzen dat AE middellijn is van de cirkel.
Trek daarvoor de lijnen MC en MG.

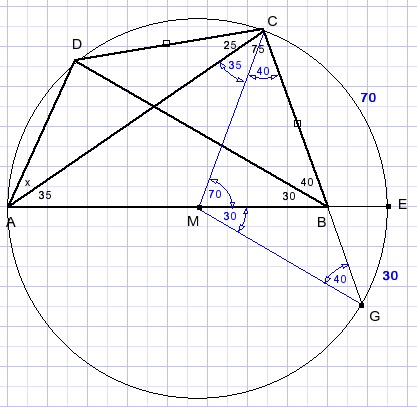
LCME = 70.
LACM = 70 - 35 = 35.... MA = MC.

LMCB = 75 - 35 = 40.
LMGC = 180 - 100 - 40 = 40.
MG = MC.

M is middelpunt van de cirkel.